TOPIC 4: THE MOLE CONCEPT AND RELATED CALCULATIONS | CHEMISTRY FORM 3
TOPIC 4: THE MOLE CONCEPT AND RELATED CALCULATIONS | CHEMISTRY FORM 3
The Mole as a Unit of Measurement
The Mole with Other Units of Measurements
Compare the mole with other units of measurements
When carrying out an experiment, a chemist cannot weigh out a single atom, ion, electron, proton or molecule of a substance. These particles are
simply very small. A counting unit that is useful in practical chemistry
must be used.
must be used.
The standard unit is called one mole of the substance. One mole of each of these different substances contains the same number of the particles (atoms, molecules, ions, electrons, protons, neutrons, etc). That number per mole has been worked by several different experimental methods and is found to be 6.0 × 1023. The value 6.0 × 1023 is called Avogadro’s constant or Avogadro’s number and is abbreviated as L. It is named after the nineteenth-century Italian chemist, Amedeo Avogadro.
The value 6.0 × 1023 is obtained through the following relationship.The mass of one atom of carbon-12 is 1.993 × 10-23g. Then, the number of atoms present in 12g of carbon-12 is derived as follows:
1 atom = 1.993 × 10-23g
X atoms = 12g
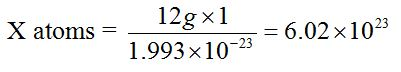
X = 6.0 × 1023 atoms.
Therefore, the number of atoms in 12g of carbon-12 and hence the number of particles in a mole are 6.02 × 1023 atoms.
Hence,
Avogadro’s number is the number of atoms in exactly 12g of carbon-12
isotope.One mole of any substance contains as many as many elementary
particles as the Avogadro’s number (constant).
Avogadro’s number is the number of atoms in exactly 12g of carbon-12
isotope.One mole of any substance contains as many as many elementary
particles as the Avogadro’s number (constant).
So, from the above explanation, the mole can be defined as the amount of a substance that contains as many elementary particles as the number of atoms present in 12g of carbon-12 isotope.
| Substance | Formula | Relative formula mass, Mr | Mass of one mole (molar mass) | This mass (1 mole) contains |
| Carbon | C | 12 | 12g | 6.0 × 1023 carbon atoms |
| Iron | Fe | 56 | 56g | 6.0 × 1023 iron atoms |
| Hydrogen | H2 | 2 × 1 = 2 | 2g | 6.0 × 1023 molecules |
| Oxygen | O2 | 2 × 16 = 32 | 32 | 6.0 × 1023 molecules |
| Water | H2O | (2×1) + 16 = 18 | 18g | 6.0 × 1023 formula units |
| Magnesium oxide | MgO | 24 + 16 = 40 | 40g | 6.0 × 1023 formula units |
| Calcium carbonate | CaCO3 | 40+12+(3×16) = 100 | 100g | 6.0 × 1023 formula units |
| Silicon oxide | SiO2 | 28 + (2 × 16) = 60 | 60g | 6.0 × 1023 formula units |
| Fe3+ | Fe3+ | 56 | 56g | 6.0 × 1023 iron(III) ions |
| Cl– | Cl– | 35.5 | 35.5g | 6.0 × 1023 chloride ions |
| e– | e– | – | – | 6.0 × 1023 electrons |
The other substances, which also exist as molecules, include ozone molecule (gas), O3; phosphorus molecule (solid), P4; sulphur molecule, S8, etc.
In
real life, when dealing with large numbers of small objects, it is
usual to count them in groups. The objects are grouped and counted in
unit amounts. For example, we buy a carton of soap, a gallon of
kerosene, a crate of soda, a dozen of pencils, a ream of papers, etc.
real life, when dealing with large numbers of small objects, it is
usual to count them in groups. The objects are grouped and counted in
unit amounts. For example, we buy a carton of soap, a gallon of
kerosene, a crate of soda, a dozen of pencils, a ream of papers, etc.
Some units of measurement
| Unit | Number of objects per unit |
| Pair | 1 pair = 2 objects, e.g. gloves, shoes, socks, scissors, etc are always sold in pairs. |
| Dozen | 1 dozen = 12 objects e.g. a dozen of cups, plates, spoons, etc. |
| Gross | 1 gross = 144 objects, e.g. a box of blackboard chalk contains 144 pieces of chalk. |
| Ream | 1 ream = 500 objects, e.g. papers are sold in reams of 500 sheets. |
| Mole | 1 mole = 6.02 ×1023 particles. In chemistry, extremely small particles are expressed in moles. For example:1 mole of atoms = 6.02 ×1023 atoms1 mole of electrons = 6.02 ×1023 electrons1 mole of protons = 6.02 ×1023 protons1 mole of ions = 6.02 ×1023 ions1 mole of molecules = 6.02 ×1023 molecules |
Molar Quantities of Different Substances
Measure molar quantities of different substances
The
mass of one mole of any substance (its molecular mass) is the atomic
mass or molecular mass expressed in grams (or kilograms). For
convenience, chemists prefer to express mass in grams, although the SI
unit of mass is the kilogram. This is because the amount of substances
which chemists usually work with in science laboratories, is quite small
and if their masses are expressed in kilograms, the numbers used would
be extremely small.
mass of one mole of any substance (its molecular mass) is the atomic
mass or molecular mass expressed in grams (or kilograms). For
convenience, chemists prefer to express mass in grams, although the SI
unit of mass is the kilogram. This is because the amount of substances
which chemists usually work with in science laboratories, is quite small
and if their masses are expressed in kilograms, the numbers used would
be extremely small.
You
can calculate the molar mass (M) of any substance by summing up the
relative atomic weights of its constituents atoms. For example, ethanol,
C2H5OH, contains two carbon atoms, six hydrogen
atoms and one oxygen atom. So, the molar mass of ethanol can be
calculated thus: Molar mass of C2H5OH = (2 × 12) + (6×1) + 16 = 46g.
can calculate the molar mass (M) of any substance by summing up the
relative atomic weights of its constituents atoms. For example, ethanol,
C2H5OH, contains two carbon atoms, six hydrogen
atoms and one oxygen atom. So, the molar mass of ethanol can be
calculated thus: Molar mass of C2H5OH = (2 × 12) + (6×1) + 16 = 46g.
In
a similar way, molar masses of other compounds can be calculated. For
example, the molar mass of sodium chloride, NaCl, is calculated by
adding together the relative atomic masses of the constituents elements
(Na = 23 and Cl = 35.5) = 23 + 35 = 58.5g (g mol-1).
a similar way, molar masses of other compounds can be calculated. For
example, the molar mass of sodium chloride, NaCl, is calculated by
adding together the relative atomic masses of the constituents elements
(Na = 23 and Cl = 35.5) = 23 + 35 = 58.5g (g mol-1).
It is important to note that relative atomic mass or relative molecular mass has no unit while molar masses are always expressed in grams or kilograms.
The molar mass of a compound is the same as the relative molecular mass and the molar mass of an element is the same as the relative atomic mass (Ar) of that element. The only difference lies in the units.
Example 1
- M(CO2) = 44g (or g mol-1) = molar mass of carbon dioxide
- Mr(CO2) = 44 = relative molecular mass of carbon dioxide
- M(Fe) = 56g (or g mol-1) molar mass of iron
- Mr(Fe) = 56 = Relative atomic mass of iron
Similarly,
the molar masses of each of the following substances can be calculated
using values for the relative atomic masses of the elements.
the molar masses of each of the following substances can be calculated
using values for the relative atomic masses of the elements.
Molar masses of different substances
| Substance | Formula | Molar mass |
| Ammonia | NH3 | 14 + 1×3 = 17g |
| Ammonium chloride | NH4Cl | 14 + (1×4) + 35.5 = 53.5g |
| Lead (II) nitrate | Pb(NO3)2 | 207 + (14×2) + (16×6) = 331g |
| Sulphuric acid | H2SO4 | (1×2) + 32 + (16×4) = 98g |
| Calcium carbonate | CaCO3 | 40 + 12 + (16×3) = 100g |
| Potassium dichromate | K2Cr2O7 | (39×2) + (52 ×2) + (16×7) = 294g |
Application of the Mole Concept
Known Masses of Elements, Molecules or Ions to Moles
Convert known masses of elements, molecules or ions to moles
In
experimental work, chemists work with varying masses. They cannot
always use one mole of a substance. The equation that links the mass of a
substance to the number of moles present is:
experimental work, chemists work with varying masses. They cannot
always use one mole of a substance. The equation that links the mass of a
substance to the number of moles present is:
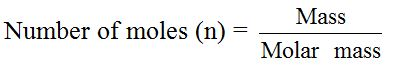
Example 2
Convert 49g of sulphuric acid, H2SO4, into moles.Given:Mass = 49g; molar mass = 98g
Formula:
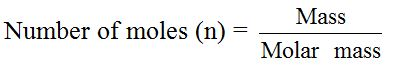
Solution:49g of H2SO4= 49/98= 0.5 mol.
Known Volumes of Gases at S.T.P to Moles
Convert known volumes of gases at S.T.P to moles
The
volume occupied by one mole of a gas at standard condition of
temperature and pressure has been scientifically determined, and it is
found to be 22.4 dm3. This volume is called the molar volume of a gas. The molar volume of a gas, therefore, has the value of 22.4 dm3 at s.t.p. Remember that 1 dm3 (1 litre) = 1000 cm3. One important thing about this value is that it applies to all gases. Therefore, at s.t.p. 32g of oxygen (O2) or 17g of ammonia (NH3) or 44g of carbon dioxide (CO2) or 40g of argon (Ar) will occupy a volume of 22.4 dm3.
This makes it easy to convert the volume of any gas at s.t.p. into
moles, or moles into volume. However, it is important to note that as
the conditions of temperature and pressure change the molar volume will
also change.
volume occupied by one mole of a gas at standard condition of
temperature and pressure has been scientifically determined, and it is
found to be 22.4 dm3. This volume is called the molar volume of a gas. The molar volume of a gas, therefore, has the value of 22.4 dm3 at s.t.p. Remember that 1 dm3 (1 litre) = 1000 cm3. One important thing about this value is that it applies to all gases. Therefore, at s.t.p. 32g of oxygen (O2) or 17g of ammonia (NH3) or 44g of carbon dioxide (CO2) or 40g of argon (Ar) will occupy a volume of 22.4 dm3.
This makes it easy to convert the volume of any gas at s.t.p. into
moles, or moles into volume. However, it is important to note that as
the conditions of temperature and pressure change the molar volume will
also change.
The number of moles of a given sample of gas is obtained by dividing the volume of the gas by molar volume (22.4 dm3).
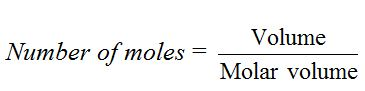
For example, 4.4d m3 of carbon dioxide gas at s.t.p. = 4.4/22.4= 0.196 mol.Similarly, 2.24 dm3 of neon gas at s.t.p. = 2.24/22.4= 0.1 mol.
If the volume of the gas is given in cm3, then it should be divided by the molar volume of a gas expressed in cm3. For example, 560 cm3 of nitrogen gas = 560cm3/22400cm3 mol= 0.025 mol.
Alternatively, the volume may, first, be converted to dm3 and then divides by the molar volume, expressed in dm3, that is, 0.46dm3/22.4dm3 = 0.25mol
Masses of Solids or Volumes of Known Gases to Actual Number of Parties
Change masses of solids or volumes of known gases to actual number of parties
The number of particles in one mole of any substance is 6.02 × 1023. To find the number of particles in a substance, we use the expression:
N = n.L, where
N = the number of particles in that substance;
n = the amount of substance (moles); and
L = the Avogadro’s constant (6.02 × 1023).
This
conversion requires two steps: first convert the mass of solid or
volume of gas to moles, and then multiply the number of moles by the
Avogadro’s constant. For example, to convert 5.6 dm3 of ammonia gas to the actual number of ammonia (NH3) molecules, change 5.6 dm3 of ammonia to moles =0.46dm3/22.4dm3=0.25 mol. Then multiply by the Avogadro’s constant to get the total number of molecules0.25 × 6.02 × 1023 = 1.5 × 1023 molecules
conversion requires two steps: first convert the mass of solid or
volume of gas to moles, and then multiply the number of moles by the
Avogadro’s constant. For example, to convert 5.6 dm3 of ammonia gas to the actual number of ammonia (NH3) molecules, change 5.6 dm3 of ammonia to moles =0.46dm3/22.4dm3=0.25 mol. Then multiply by the Avogadro’s constant to get the total number of molecules0.25 × 6.02 × 1023 = 1.5 × 1023 molecules
Similarly, 1.12 dm3 of hydrogen gas = 1.12/22.4= 0.05 mol. This is equal to 0.05 × 6.02 × 1023 = 3.0 ×1022 molecules
Alternatively,
we may find out the number of particles by converting the given volume
to the number of molecules straight forward without passing through the
number of moles first. We know that one mole (22.4 dm3) of a gas at s.t.p. = 6.02 × 1023 molecules. So, 5.6 dm3 = 5.6×6.02 × 1023/22.4= 1.5 × 1023 molecules
we may find out the number of particles by converting the given volume
to the number of molecules straight forward without passing through the
number of moles first. We know that one mole (22.4 dm3) of a gas at s.t.p. = 6.02 × 1023 molecules. So, 5.6 dm3 = 5.6×6.02 × 1023/22.4= 1.5 × 1023 molecules
Molar Solutions of Various Soluble Substances
Prepare molar solutions of various soluble substances
A molar solution is a solution which contains one of the compound in one litre (1 dm3 or 1000 cm3)
of the solution.Let us consider the case of sodium hydroxide, NaOH. The
molecular weight of this compound is 40g. Therefore, a molar solution
of sodium hydroxide will contain 40g in 1000 cm3(1 dm3) of the solution.
of the solution.Let us consider the case of sodium hydroxide, NaOH. The
molecular weight of this compound is 40g. Therefore, a molar solution
of sodium hydroxide will contain 40g in 1000 cm3(1 dm3) of the solution.
Also, consider anhydrous sodium carbonate, Na2CO3. 1 mole of this carbonate weights 106g. Hence, its molar solution will contain 106g of the anhydrous salt in 1000 cm3 of solution.If, however, 0.1 moles (10.6g) of the solute is dissolved in 1.0 dm3, the solution is 0.1 molar. But if 0.1 moles is dissolved in 0.1 dm3 of the solution, the solution is still 1.0 molar (since 1 dm3 of solution would contain 1.0 mole of the solute).
The molecular weights of some common substances are shown below:
| Compound | Molecular weight (1 mole) |
| Potassium hydroxide, NaOH | 56g |
| Hydrochloric acid, HCl | 36.5g |
| Sulphuric acid, H2SO4 | 98g |
| Sodium chloride, NaCl | 58.5g |
| Sodium bicarbonate, NaHCO3 | 84g |
| Calcium hydroxide, Ca(OH)2 | 74g |
The molar solution of each of these substances can be prepared by dissolving one mole of each substance in 1000 cm3 (1 dm3) of distilled water. We see, therefore, that 40g of sodium hydroxide in 1000 cm3
of solution will give a 1.0M solution. Hence, 20g of the hydroxide
should give a 0.5M solution. In a similar way, we can make derivative
solution concentrations ranging as follows: 0.1M, 0.2M, 0.3M, 0.4M….1M,
2M, etc.
of solution will give a 1.0M solution. Hence, 20g of the hydroxide
should give a 0.5M solution. In a similar way, we can make derivative
solution concentrations ranging as follows: 0.1M, 0.2M, 0.3M, 0.4M….1M,
2M, etc.
However, in each case the amount of solution should always be 1000 cm3. The concentration ranges like these are known as molarities of solutions. Hence, 0.5M sodium carbonate can also be read as “a sodium carbonate solution with a molarity of 0.5M.”
The Concentration of Solutions
When
a chemical substance (the solute) is dissolved in a given volume of
solvent, we can measure the “quantity” of solute in two ways; we can
measure either its mass (in grams) or its amount (in moles). The final volume of the solution is usually measured in dm3.
a chemical substance (the solute) is dissolved in a given volume of
solvent, we can measure the “quantity” of solute in two ways; we can
measure either its mass (in grams) or its amount (in moles). The final volume of the solution is usually measured in dm3.
When we measure the mass of the solute in grams, we obtainthe mass concentration in g/dm3
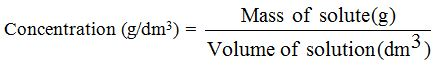
Example 3
Calculate the concentration (g/dm3) of sodium chloride solution (NaCl) that contains 20g of sodium chloride in a final solution of 100 cm3
Solution
First, convert the given volume to dm3
Volume (dm3) = 100/1000= 0.1 dm3
Then, work out the concentration of the solution by dividing the mass (weight) of solute (g) by the volume (dm3).
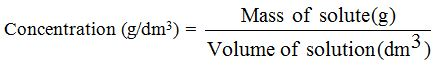
=20g/0.1dm3
= 200g/dm3
Alternatively, we could calculate the concentration straightforward without having to convert the given volume into dm3, e.g.:If 20g of the solution are contained in 100 cm3 of the solution, then the amount of solute in 1000 cm3 (1 dm3) of the solution would be
1000×20/100 = 200g/dm3
Calculations Based on the Mole Concept
Perform calculations based on the mole concept
A
chemist always wants to know how much of one substance would react with
a given amount of another substance. This is achieved by use of
balanced chemical equations. Such equations are called stoichiometric
equations.
chemist always wants to know how much of one substance would react with
a given amount of another substance. This is achieved by use of
balanced chemical equations. Such equations are called stoichiometric
equations.
A
stoichiometric equation is the one in which the reactants and the
products are correctly balanced; all the atoms, ions and electrons are
conserved. Such an equation gives correct mole ratios of reactants and
products in chemical reactions. This quantitative relationship is called
stoichiometry.
stoichiometric equation is the one in which the reactants and the
products are correctly balanced; all the atoms, ions and electrons are
conserved. Such an equation gives correct mole ratios of reactants and
products in chemical reactions. This quantitative relationship is called
stoichiometry.
Consider an equation for the reaction between hydrogen and nitrogen to produce ammonia:
3H2(g) + N2(g)→ 2NH3
This can be read as follows:
three moles of hydrogen reacts with one mole of nitrogen to yield two moles of ammonia.
The
numbers 3, 1 and 2 are called stoichiometric coefficients. They tell us
the proportions in which the substances react and in which the products
are formed.
numbers 3, 1 and 2 are called stoichiometric coefficients. They tell us
the proportions in which the substances react and in which the products
are formed.
Example 4
What volume of carbon dioxide (CO2) measured at s.t.p. will be produced when 21.0g of sodium hydrogencarbonate (NaHCO3) is completely decomposed according to the equation.2NaHCO3(s)→ Na2CO3(s) + CO2(g) + H2O(l)
Solution
First, find the weight of carbon dioxide that will be produced by the hydrogencarbonate.
- Mass of 2NaHCO3 = 2 × 84 = 168g
- Mass of CO2 = 44g
The weight of carbon dioxide produced can be obtained from the following relation:
168g ≡ 44g
21g ≡ X
X = 21×44/168 = 5.5g
The weight of carbon dioxide produced = 5.5g
Then, convert this weight of CO2 to volume at s.t.p.We know that one mole (44g) of carbon dioxide at s.t.p. occupies 22.4 dm3
That is, 44g ≡ 22.4dm3
5.5g ≡ X dm3
X = 5.5×22.4/44 = 2.8dm3






