TOPIC 8: PYTHAGORAS THEOREM ~ MATHEMATICS FORM 2
TOPIC 8: PYTHAGORAS THEOREM ~ MATHEMATICS FORM 2
Pythagoras Theorem
Triangle with a Right angle i.e. 90° has an amazing property. Do you want to know what property is that? Go on, read our notes to see the amazing property of a right angled triangle.
Pythagoras Theorem deals only with problems involving any Triangle having one of its Angles with 900. This kind of a Triangle is called Right angled triangle. When triangle is a right angled triangle, squares can be made on each of the three sides. See illustration below:
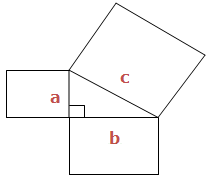
The Area of the biggest square is exact the same as the sum of the other two squares put together. This is what is called Pythagoras theorem and it is written as:
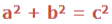
that is:
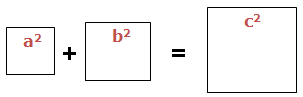
‘c’ is the Longest side of the Triangle, is called Hypogenous and is the one that forms the biggest square. a and b are the two smaller sides.
Proof of Pythagoras Theorem
The Pythagoras Theorem
Prove the pythagoras theorem
Pythagoras
theorem states that: In a Right Angled Triangle, the sum of squares of
smaller sides is exactly equal to the square of Hypotenuse side (large
side). i.e. a2 + b2 = c2
theorem states that: In a Right Angled Triangle, the sum of squares of
smaller sides is exactly equal to the square of Hypotenuse side (large
side). i.e. a2 + b2 = c2
Take a look on how to show that a2 + b2 = c2
See the figure below:
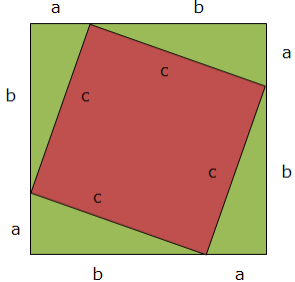
The area of a whole square (big square)
A big square is the one with sides a + b each. Its area will be:
(a + b) ×(a + b)
Area of the other pieces
First, area of a smaller square (tilted) = c2
Second, area of the equal triangles each with bases a and height b:
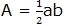
But there are 4 triangles and they are equal, so total area =
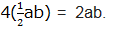
Both areas must be equal, the area of a big square must be equal to the area of a tilted square plus the area of 4 triangles
That is:
(a + b)(a + b) = c2 + 2ab
Expand (a +b)(a + b): a2 +2ab + b2 = c2 + 2ab
Subtract 2ab from both sides: a2 + b2 = c2 Hence the result!
Note: We can use Pythagoras theorem to solve any problem that can be converted into right Angled Triangle.
Exercise 1
1. In a right triangle with given hypotenuse c and legs a and b, find:
- c if a = 5 and b = 12
- a if b = 8 and c = 12
- b if a = 9 and c = 11
2. A rectangle has base 6 and height 10. What is the length of the diagonal?
3. A square has a diagonal with length 6. What is the length of the sides of the square?
4. The diagonals of a rhombus have lengths 6 and 8. Find the length of one side of the rhombus.
5.
A ladder leans against a wall. If the ladder reaches 8m up the wall and
its foot is 6m from the base of the wall. Find the length of the
ladder.
A ladder leans against a wall. If the ladder reaches 8m up the wall and
its foot is 6m from the base of the wall. Find the length of the
ladder.
6. Find the value of the marked side.
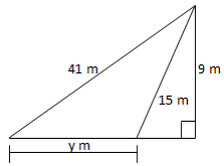
The Pythagoras Theorem
Prove the pythagoras theorem
Pythagoras
theorem states that: In a Right Angled Triangle, the sum of squares of
smaller sides is exactly equal to the square of Hypotenuse side (large
side). i.e. a2 + b2 = c2
theorem states that: In a Right Angled Triangle, the sum of squares of
smaller sides is exactly equal to the square of Hypotenuse side (large
side). i.e. a2 + b2 = c2
Take a look on how to show that a2 + b2 = c2
See the figure below:

The area of a whole square (big square)
A big square is the one with sides a + b each. Its area will be:
(a + b) ×(a + b)
Area of the other pieces
First, area of a smaller square (tilted) = c2
Second, area of the equal triangles each with bases a and height b:
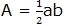
But there are 4 triangles and they are equal, so total area =
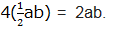
Both areas must be equal, the area of a big square must be equal to the area of a tilted square plus the area of 4 triangles
That is:
(a + b)(a + b) = c2 + 2ab
Expand (a +b)(a + b): a2 +2ab + b2 = c2 + 2ab
Subtract 2ab from both sides: a2 + b2 = c2 Hence the result!
Note: We can use Pythagoras theorem to solve any problem that can be converted into right Angled Triangle.
Exercise 1
1. In a right triangle with given hypotenuse c and legs a and b, find:
- c if a = 5 and b = 12
- a if b = 8 and c = 12
- b if a = 9 and c = 11
2. A rectangle has base 6 and height 10. What is the length of the diagonal?
3. A square has a diagonal with length 6. What is the length
Application of Pythagoras Theorem
The Pythagoras Theorem to Solve Daily Life Problems
Apply the pythagoras theorem to solve daily life problems
You
may have heard about Pythagoras’s theorem (or the Pythagorean Theorem)
in your math class, but what you may fail to realize is that
Pythagoras’s theorem is used often in real life situations. For example,
calculating the distance of a road, television or smart phone screen
size (usually measured diagonally).
may have heard about Pythagoras’s theorem (or the Pythagorean Theorem)
in your math class, but what you may fail to realize is that
Pythagoras’s theorem is used often in real life situations. For example,
calculating the distance of a road, television or smart phone screen
size (usually measured diagonally).
Activity 1
Apply the pythagoras theorem to solve daily life problems







I like it