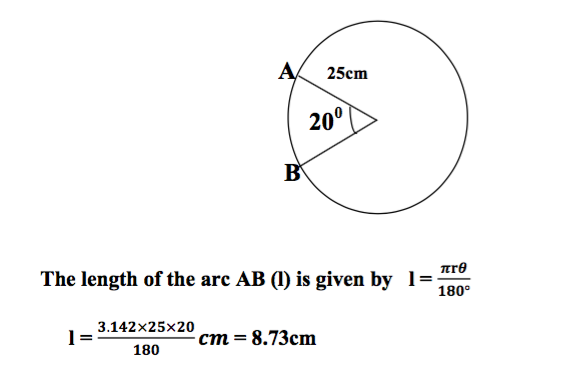
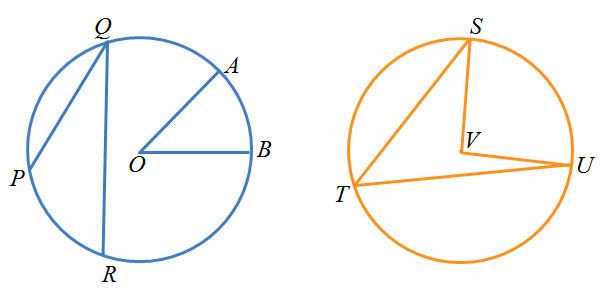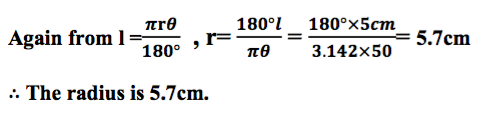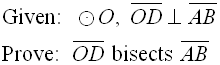TOPIC 6: CIRCLES ~ MATHEMATICS FORM 3
TOPIC 6: CIRCLES ~ MATHEMATICS FORM 3
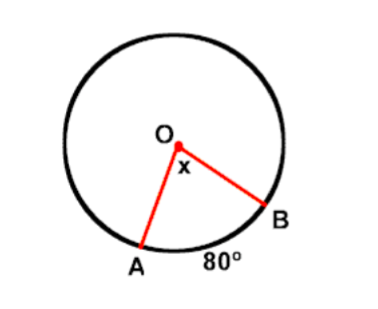
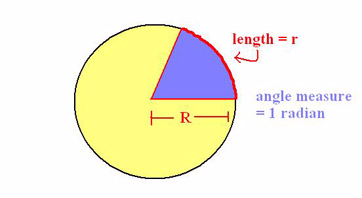
Definition of Terms
A Tangent to a Circle
Describe a tangent to a circle
Tangent
is a line which touches a circle. The point where the line touches the
circle is called the point of contact. A tangent is perpendicular to the
radius at the point of contact.
is a line which touches a circle. The point where the line touches the
circle is called the point of contact. A tangent is perpendicular to the
radius at the point of contact.
Tangent Properties of a Circle
Identify tangent properties of a circle
A
tangent to a circle is perpendicular to the radius at the point of
tangency. A common tangent is a line that is a tangent to each of two
circles. A common external tangent does not intersect the segment that
joins the centers of the circles. A common internal tangent intersects
the segment that joins the centers of the circles.
tangent to a circle is perpendicular to the radius at the point of
tangency. A common tangent is a line that is a tangent to each of two
circles. A common external tangent does not intersect the segment that
joins the centers of the circles. A common internal tangent intersects
the segment that joins the centers of the circles.
Tangent Theorems
Prove tangent theorems
Theorem 1
If
two chords intersect in a circle, the product of the lengths of the
segments of one chord equal the product of the segments of the other.
two chords intersect in a circle, the product of the lengths of the
segments of one chord equal the product of the segments of the other.
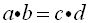
Intersecting Chords Rule: (segment piece)×(segment piece) =(segment piece)×(segment piece)
Theorem Proof:
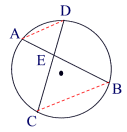
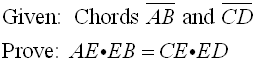
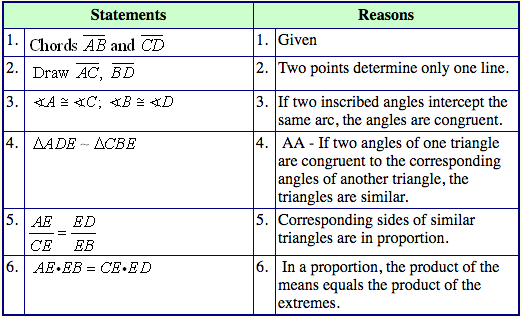
Theorem 2:
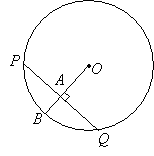
If
two secant segments are drawn to a circle from the same external point,
the product of the length of one secant segment and its external part
is equal to the product of the length of the other secant segment and
its external part.
two secant segments are drawn to a circle from the same external point,
the product of the length of one secant segment and its external part
is equal to the product of the length of the other secant segment and
its external part.
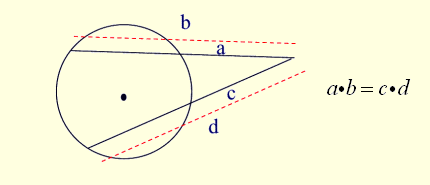
Secant-Secant Rule: (whole secant)×(external part) =(whole secant)×(external part)
Theorem 3:
If
a secant segment and tangent segment are drawn to a circle from the
same external point, the product of the length of the secant segment and
its external part equals the square of the length of the tangent
segment.
a secant segment and tangent segment are drawn to a circle from the
same external point, the product of the length of the secant segment and
its external part equals the square of the length of the tangent
segment.
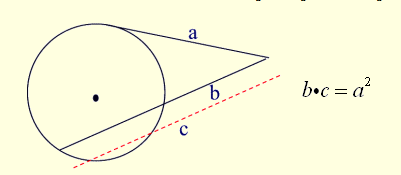
Secant-Tangent Rule:(whole secant)×(external part) =(tangent)2
Theorems Relating to Tangent to a Circle in Solving Problems
Apply theorems relating to tangent to a circle in solving problems
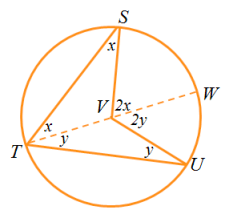
Example 7
Two
common tangents to a circle form a minor arc with a central angle of
140 degrees. Find the angle formed between the tangents.
common tangents to a circle form a minor arc with a central angle of
140 degrees. Find the angle formed between the tangents.
Solution
Two tangents and two radii form a figure with 360°. If y is the angle formed between the tangents then y + 2(90) + 140° = 360°
y = 40°.
The angle formed between tangents is 40 degrees.