NUMBERS ~ MATHEMATICS FORM 1
NUMBERS ~ MATHEMATICS FORM 1
We know that when we count we start 1,2 …. . But there are other numbers
like 0, negative numbers and decimals.
All these types of numbers are categorized in different groups like counting numbers, integers,real numbers, whole numbers and rational and irrational numbers according to their properties.
all these have been covered in this chapter
NUMBERS ~ MATHEMATICS FORM 1
Integers
Integers
Identify integers
Consider a number line below
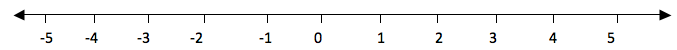
The
numbers from 0 to the right are called positive numbers and the numbers
from 0 to the left with minus (-) sign are called negative numbers.
Therefore all numbers with positive (+) or negative (-) sign are called
integers and they are denoted by Ζ. Numbers with positive sign are
written without showing the positive sign. For example +1, +2, +3, …
they are written simply as 1, 2, 3, … . But negative numbers must carry
negative sign (-). Therefore integers are all positive and negative
numbers including zero (0). Zero is neither positive nor negative
number. It is neutral.
numbers from 0 to the right are called positive numbers and the numbers
from 0 to the left with minus (-) sign are called negative numbers.
Therefore all numbers with positive (+) or negative (-) sign are called
integers and they are denoted by Ζ. Numbers with positive sign are
written without showing the positive sign. For example +1, +2, +3, …
they are written simply as 1, 2, 3, … . But negative numbers must carry
negative sign (-). Therefore integers are all positive and negative
numbers including zero (0). Zero is neither positive nor negative
number. It is neutral.
NUMBERS ~ MATHEMATICS FORM 1
The
numbers from zero to the right increases their values as the increase.
While the numbers from zero to the left decrease their values as they
increase. Consider a number line below.
numbers from zero to the right increases their values as the increase.
While the numbers from zero to the left decrease their values as they
increase. Consider a number line below.
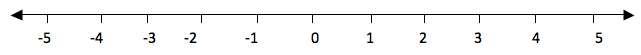
If
you take the numbers 2 and 3, 3 is to the right of 2, so 3 is greater
than 2. We use the symbol ‘>’ to show that the number is greater than
i. e. 3 >2(three is greater than two). And since 2 is to the left of
3, we say that 2 is smaller than 3 i.e. 2<3. The symbol ‘<’ is
use to show that the number is less than.
you take the numbers 2 and 3, 3 is to the right of 2, so 3 is greater
than 2. We use the symbol ‘>’ to show that the number is greater than
i. e. 3 >2(three is greater than two). And since 2 is to the left of
3, we say that 2 is smaller than 3 i.e. 2<3. The symbol ‘<’ is
use to show that the number is less than.
Consider
numbers to the left of 0. For example if you take -5 and -3. -5 is to
the left of -3, therefore -5 is smaller than -3. -3 is to the right of
-5, therefore -3 is greater than -5.
numbers to the left of 0. For example if you take -5 and -3. -5 is to
the left of -3, therefore -5 is smaller than -3. -3 is to the right of
-5, therefore -3 is greater than -5.
Generally, the number which is to the right of the other number is greater than the number which is to the left of it.
If
two numbers are not equal to each to each other, we use the symbol ‘≠’
to show that the two numbers are not equal. The not equal to ‘≠’ is the
opposite of is equal to ‘=’.
two numbers are not equal to each to each other, we use the symbol ‘≠’
to show that the two numbers are not equal. The not equal to ‘≠’ is the
opposite of is equal to ‘=’.
Example 21
Represent the following integers Ζ on a number line
- 0 is greater than Ζ and Ζ is greater than -4
- -2 is less than Ζ and Ζ is less than or equal to 1.
NUMBERS ~ MATHEMATICS FORM 1
Solution
a.
0 is greater than Ζ means the integers to the left of zero and Ζ is
greater than -4 means integers to the left of -4. These numbers are -1,
-2 and -3. Consider number line below
0 is greater than Ζ means the integers to the left of zero and Ζ is
greater than -4 means integers to the left of -4. These numbers are -1,
-2 and -3. Consider number line below
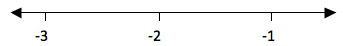
b.
-2 is less than Ζ means integers to the right of -2 and Ζ is less than
or equal to 1 means integers to the left of 1 including 1. These
integers are -1, 0 and 1. Consider the number line below
-2 is less than Ζ means integers to the right of -2 and Ζ is less than
or equal to 1 means integers to the left of 1 including 1. These
integers are -1, 0 and 1. Consider the number line below
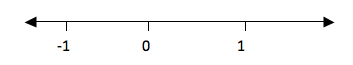
Example 22
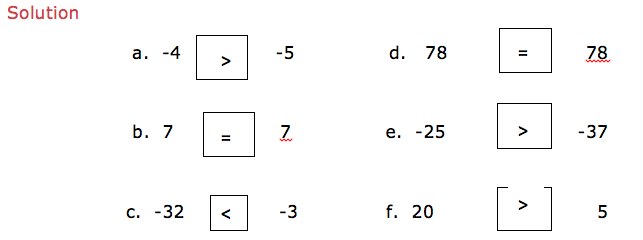
Put the signs ‘is greater than’ (>), ‘is less than’ (<), ‘is equal to’ (=) to make a true statement.
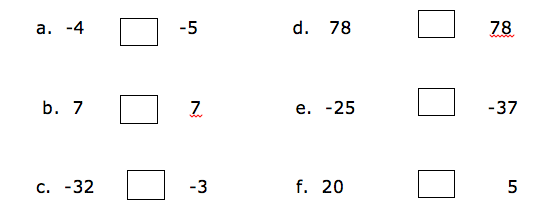
Addition of Integers
Add integers
NUMBERS ~ MATHEMATICS FORM 1
Example 23
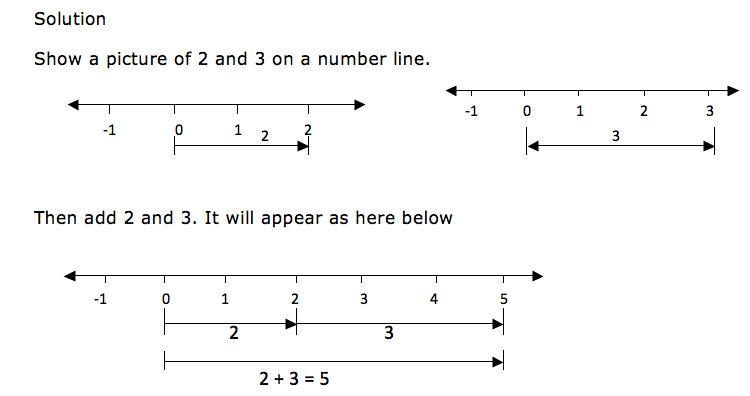
2 + 3
Show a picture of 2 and 3 on a number line.
When
drawing integers on a number line, the arrows for the positive numbers
goes to the right while the arrows for the negative numbers goes to the
left. Consider an illustration bellow.
drawing integers on a number line, the arrows for the positive numbers
goes to the right while the arrows for the negative numbers goes to the
left. Consider an illustration bellow.
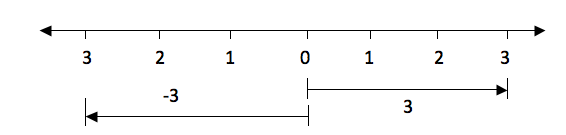
The
distance from 0 to 3 is the same as the distance from 0 to -3, only the
directions of their arrows differ.
distance from 0 to 3 is the same as the distance from 0 to -3, only the
directions of their arrows differ.
NUMBERS ~ MATHEMATICS FORM 1
The arrow for positive 3 goes to the
right while the arrow for the negative 3 goes to the left.
Example 24
-3 + 6
Solution
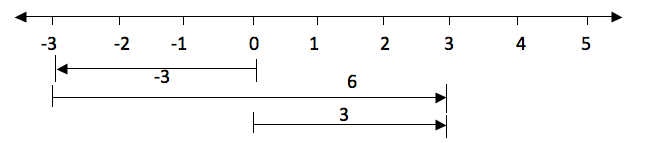
-
Subtraction of IntegersSubtract integersSince
subtraction is the opposite of addition, if for example you are given
5-4 is the same as 5 + (-4). So if we have to subtract 4 from 5 we can
use a number line in the same way as we did in addition. Therefore 5-4
on a number line will be: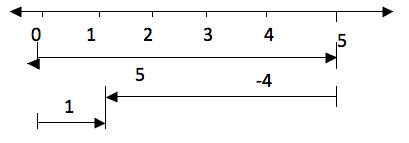 Take five steps from 0 to the right and then four steps to the left from 5. The result is 1.
Take five steps from 0 to the right and then four steps to the left from 5. The result is 1.NUMBERS ~ MATHEMATICS FORM 1
Multiplication of Integers
Multiply integersExample 252×6 is the same as add 2 six times i.e. 2×6 = 2 + 2 + 2 + 2 + 2 +2 = 12. On a number line will be: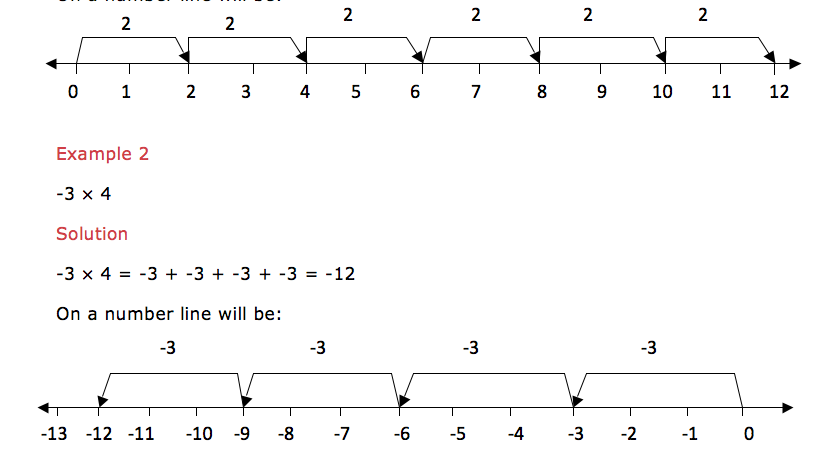 Multiplication
Multiplication
of a negative integer by a negative integer cannot be shown on a number
line but the product of these two negative integers is a positive
integer.From
the above examples we note that multiplication of two positive integers is a positive integer. And multiplication of a positive integer by a negative integer is a negative integer. In summary:NUMBERS ~ MATHEMATICS FORM 1
- (+)×,(+) = (+)
- (-)×,(-) = (+)
- (+)×,(-) = (-)
- (-)×,(+) = (-)
-
Division of IntegersDivide integersExample 266÷3 is the same as saying that, which number when you multiply it by 3 you will get 6, that number is 2, so, 6÷3 = 2.Therefore
division is the opposite of multiplication. From our example 2×3 = 6
and 6÷3 = 2. Thus multiplication and division are opposite to each
other.Dividing
two integers which are both positive the quotient (answer) is a
positive integer. If they are both negative also the quotient is
positive. If one of the integer is positive and the other is negative
then the quotient is negative. In summary:- (+)÷(+) = (+)
- (-)÷(-) = (+)
- (+)÷(-) = (-)
- (-)÷(+) = (-)
Mixed Operations on IntegersPerform mixed operations on integersYou
may be given more than one operation on the same problem.NUMBERS ~ MATHEMATICS FORM 1
Do
multiplication and division first and then the rest of the signs. If
there are brackets, we first open the brackets and then we do division
followed by multiplication, addition and lastly subtraction. In short we
call it BODMAS. The same as the one we did on operations on whole
numbers.NUMBERS ~ MATHEMATICS FORM 1
Example 27
9÷3 + 3×2 -1 =Solution9÷3 + 3×2 -1=3 + 6 -1 (first divide and multiply)=8 (add and then subtract)Example 28(12÷4 -2) + 4 – 7=
Solution(12÷4 -2) + 4 – 7=1 + 4 – 7 (do operations inside the brackets and divide first)=5 – 7 (add)=2
NUMBERS ~ MATHEMATICS FORM 1











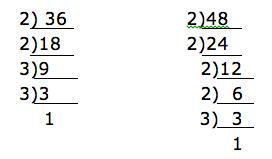
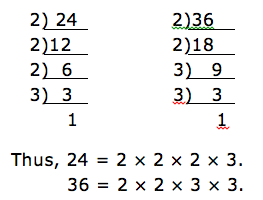





Wonderful, what a web site it is! This blog gives helpful facts to us, keep it up.
Magnificent goods from you, man. I have understand your stuff previous
to and you are just too excellent. I actually like what you’ve acquired here,
certainly like what you’re saying and the way in which you say
it. You make it enjoyable and you still take care of to keep it
smart. I can’t wait to read far more from you. This is really a
tremendous site.
Hey there! I’m at work browsing your blog from my new apple
iphone! Just wanted to say I love reading through your blog and look forward to
all your posts! Keep up the great work!
I visited several websites except the audio quality for audio songs existing at
this website is in fact marvelous. 0mniartist asmr
It’s an amazing post designed for all the internet
users; they will take benefit from it I am sure. asmr 0mniartist
Hello there! I just want to offer you a big thumbs up for your great info
you’ve got here on this post. I will be coming back to your web site for
more soon. 0mniartist asmr
Woah! I’m really digging the template/theme of this blog.
It’s simple, yet effective. A lot of times it’s tough to get that “perfect balance” between usability and appearance.
I must say that you’ve done a very good job with
this. Additionally, the blog loads very quick for me on Firefox.
Outstanding Blog! asmr 0mniartist
You actually make it seem so easy together with your presentation however I find this topic to be really something which
I think I’d never understand. It seems too complicated and extremely wide
for me. I am looking ahead in your next submit, I’ll attempt to
get the hold of it! asmr 0mniartist
Well explained …hongera sana