Table of Contents
ToggleTOPIC 1: COORDINATE GEOMETRY ~ MATHEMATICS FORM 4
TOPIC 1: COORDINATE GEOMETRY ~ MATHEMATICS FORM 4
Equation of a Line
The General Equation of a Straight Line
Derive the general equation of a straight line
COORDINATES OF A POINT
•The coordinates of a points – are the values of x and y enclosed by the brackets which are used to describe the position of point in a line in the plane.
The plane is called xy-plane and it has two axis.
- horizontal axis known as axis and
- vertical axis known as axis
Consider the xy-plane below
The coordinates of points A, B, C ,D and E are A(2, 3), B(4, 4), C(-3, -1), D(2, -4) and E(1, 0).
Definition

Example 1
Find the gradient of the lines joining
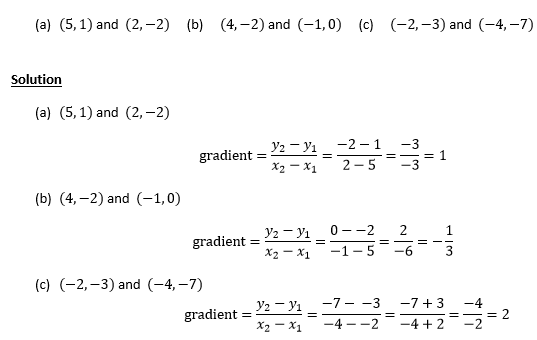
Example 2
(a) The line joining (2, -3) and (k, 5) has a gradient -2. Find k

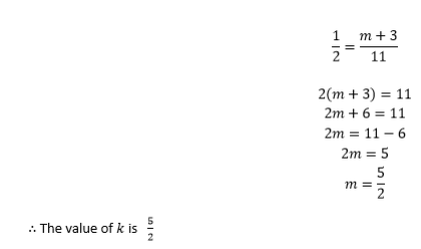
Exercise 1
1. Find the gradientof the line which passes through the following points ;
- (3,6) and (-2,8)
- (0,6) and (99,-12)
- (4,5)and (5,4)
2. A line passes through (3, a) and (4, -2), what is the value of a if the slope of the line is 4?
3. The gradient of the linewhich goes through (4,3) and (-5,k) is 2. Find the value of k.
FINDING THE EQUATION OF A STRAIGHT LINE
The equation of a straight line can be determined if one of the following is given:-
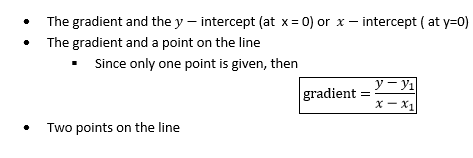
Example 3
Find the equation of the line with the following
- Gradient 2 and intercept
- Gradient and passing through the point
- Passing through the points and
Solution


EQUATION OF A STRAIGHT LINE IN DIFFERENT FORMS
The equation of a line can be expressed in two forms

Example 4
INTERCEPTS

Therefore

Example 5
Find the y-intercept of the following lines

Example 6
Find the x and y-intercept of the following lines


Exercise 2
Attempt the following Questions.
- Find the y-intercept of the line 3x+2y = 18 .
- What is the x-intercept of the line passing through (3,3) and (-4,9)?
- Calculate the slope of the line given by the equation x-3y= 9
- Find the equation of the straight line with a slope -4 and passing through the point (0,0).
- Find the equation of the straight line with y-intercept 5 and passing through the point (-4,8).
GRAPHS OF STRAIGHT LINES
The graph of straight line can be drawn by using the following methods;
- By using intercepts
- By using the table of values
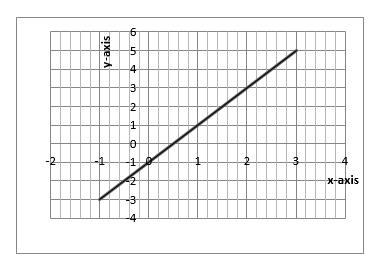
Example 7
Sketch the graph of Y = 2X – 1

SOLVING SIMULTANEOUS EQUATION BY GRAPHICAL METHOD
- Use the intercepts to plot the straight lines of the simultaneous equations
- The point where the two lines cross each other is the solution to the simultaneous equations
Example 8
Solve the following simultaneous equations by graphical method

Exercise 3
1. Draw the line 4x-2y=7 and 3x+y=7 on the same axis and hence determine their intersection point
2. Find the solutionfor each pair the following simultaneous equations by graphical method;
- y-x = 3 and 2x+y = 9
- 3x- 4y=-1 and x+y = 2
- x = 8 and 2x-3y = 10
Midpoint of a Line Segment
The Coordinates of the Midpoint of a Line Segment
Determine the coordinates of the midpoint of a line segment
Let S be a point with coordinates (x1,y1), T with coordinates (x2,y2) and M with coordinates (x,y) where M is the mid-point of ST. Consider the figure below:
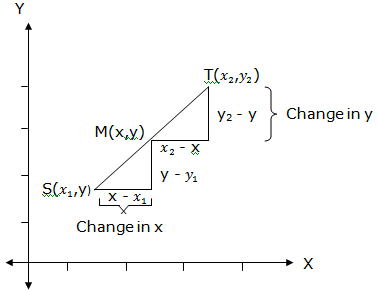
Considering the angles of the triangles SMC and TMD, the triangles SMC and TMD are similar since their equiangular

Example 9
Find the coordinates of the mid-point joining the points (-2,8) and (-4,-2)
Solution
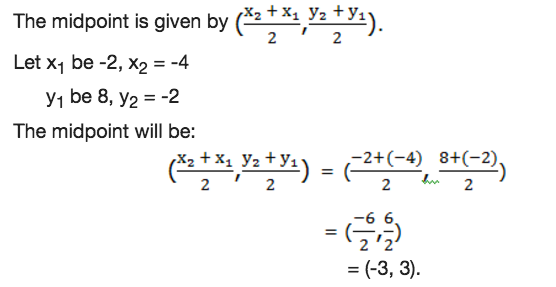
Therefore the coordinates of the midpoint of the line joining the points (-2,8) and (-4, -2) is (-3,3).
Distance Between Two Points on a Plane
The Distance Between Two Points on a Plane
Calculate the distance between two points on a plane
Consider two points, A(x1,y1) and B(x2,y2) as shown in the figure below:
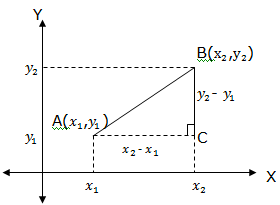
The distance between A and B in terms of x1, y1,x2, and y2can be found as follows:Join AB and draw doted lines as shown in the figure above.
Then, AC = x2– x1and BC = y2– y1
Since the triangle ABC is a right angled, then by applying Pythagoras theorem to the triangle ABC we obtain

Therefore the distance is 13 units.
Parallel and Perpendicular Lines
Gradients in order to Determine the Conditions for any Two Lines to be Parallel
Compute gradients in order to determine the conditions for any two lines to be parallel
The two lines which never meet when produced infinitely are called parallel lines. See figure below:
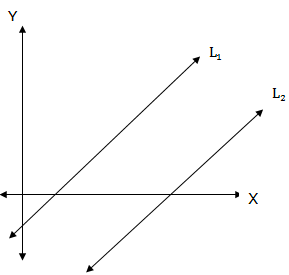
The two parallel lines must have the same slope. That is, if M1is the slope for L1and M2is the slope for L2thenM1= M2
Gradients in order to Determine the Conditions for any Two Lines to be Perpendicular
Compute gradients in order to determine the conditions for any two lines to be perpendicular
When two straight lines intersect at right angle, we say that the lines are perpendicular lines. See an illustration below.
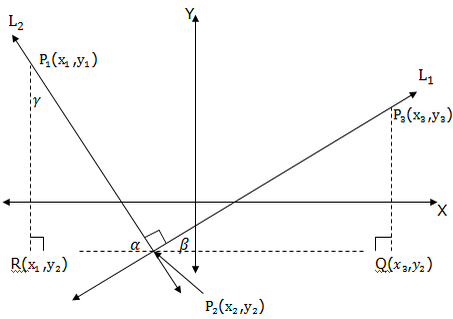
Consider the points P1(x1,y1), P2(x2,y2), P3(x3,y3), R(x1,y2) and Q(x3,y2) and the anglesα,β,γ(alpha, beta and gamma respectively).
- α+β = 90 (complementary angles)
- α+γ= 90 (complementary angles)
- β = γ (alternate interior angles)
Therefore the triangle P2QP3is similar to triangle P1RP2.
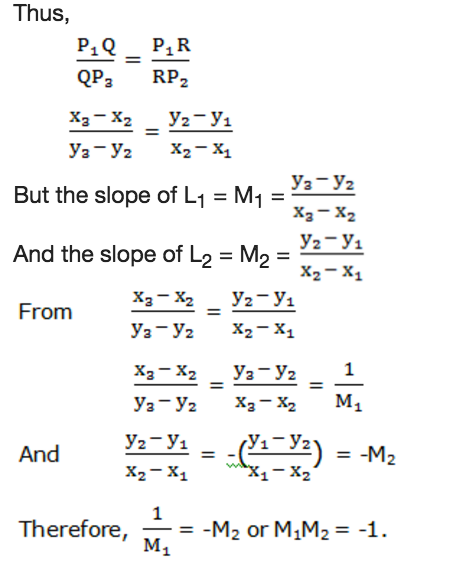
Generally two perpendicular lines L1and L2with slopes M1and M2respectively the product of their slopes is equal to negative one. That is M1M2= -1.
Example 10
Show that A(-3,1), B(1,2), C(0,-1) and D(-4,-2) are vertices of a parallelogram.
Solution
Let us find the slope of the lines AB, DC, AD and BC

We
see that each two opposite sides of the parallelogram have equal slope.
This means that the two opposite sides are parallel to each other,
which is the distinctive feature of the parallelogram. Therefore the
given vertices are the vertices of a parallelogram.
see that each two opposite sides of the parallelogram have equal slope.
This means that the two opposite sides are parallel to each other,
which is the distinctive feature of the parallelogram. Therefore the
given vertices are the vertices of a parallelogram.
Problems on Parallel and Perpendicular Lines
Solve problems on parallel and perpendicular lines
Example 11
Show that A(-3,2), B(5,6) and C(7,2) are vertices of a right angled triangle.
Solution
Right
angled triangle has two sides that are perpendicular, they form 90°.We
know that the slope of the line is given by: slope = change in y/change
in x
angled triangle has two sides that are perpendicular, they form 90°.We
know that the slope of the line is given by: slope = change in y/change
in x
Now,
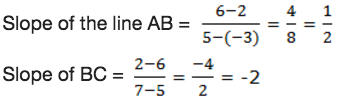
Since the slope of AB and BC are negative reciprocals, then the triangle ABC is a right angled triangle at B.



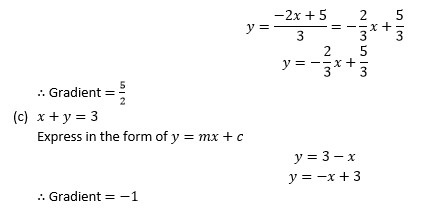
Saved as a favorite, I love your site!
Hello friends, how is the whole thing, and what you want to
say on the topic of this article, in my view its genuinely amazing in support of me.
This is the right webpage for everyone who wishes to understand this topic.
You know so much its almost hard to argue with you (not that I actually
would want to…HaHa). You definitely put a new spin on a topic that has been written about for years.
Wonderful stuff, just great!
Hi there! Someone in my Facebook group shared this site with us so I
came to check it out. I’m definitely enjoying the information. I’m bookmarking
and will be tweeting this to my followers! Exceptional blog and great design and style.
Hello my loved one! I wish to say that this article is awesome, great written and include approximately
all significant infos. I would like to look more posts like this .
At this time I am going away to do my breakfast, afterward having my breakfast coming again to read other
news.
Hey there this is somewhat of off topic but I was wanting
to know if blogs use WYSIWYG editors or if you have to manually code with HTML.
I’m starting a blog soon but have no coding skills so I wanted to get advice from someone with experience.
Any help would be enormously appreciated!
I’m not sure where you are getting your information, but great topic.
I needs to spend some time learning more or understanding more.
Thanks for magnificent info I was looking for this information for my mission.
This is really interesting, You’re a very skilled blogger. I’ve joined your rss feed
and look forward to seeking more of your magnificent post.
Also, I’ve shared your web site in my social networks!
I used to be able to find good info from your articles.
Everything is very open with a really clear explanation of the issues.
It was truly informative. Your website is very helpful.
Many thanks for sharing!
Hi to every one, the contents present at this site are genuinely
amazing for people knowledge, well, keep up the good work fellows.
My brother recommended I may like this web site.
He used to be totally right. This put up actually made my day.
You cann’t imagine just how much time I had spent for
this information! Thank you!
Hello my friend! I want to say that this article is amazing,
nice written and come with approximately all vital infos. I would like to look extra
posts like this .
Thanks for another informative website. The place else may
I get that type of information written in such an ideal manner?
I’ve a venture that I’m simply now operating on, and I have
been at the look out for such info.
Thank you a lot for sharing this with all folks you really know
what you’re speaking about! Bookmarked. Kindly also consult with my web site =).
We will have a link alternate arrangement between us
Way cool! Some very valid points! I appreciate you writing this post and the rest of the website is very good.
Wow! After all I got a web site from where I be able to genuinely take useful facts concerning my study and knowledge.
Hello, its good post on the topic of media print, we all be familiar with media is a fantastic source of data.
Hi to all, it’s genuinely a nice for me to pay a quick
visit this site, it contains helpful Information.
We are a group of volunteers and opening a new scheme in our community.
Your site offered us with valuable info to work on. You’ve done an impressive job and our entire community
will be grateful to you.
This piece of writing is really a nice one it assists new net visitors, who are
wishing in favor of blogging.
Greetings from Idaho! I’m bored at work so I decided
to browse your site on my iphone during lunch break. I love the info you provide here and can’t wait to take a look when I get home.
I’m shocked at how quick your blog loaded on my phone ..
I’m not even using WIFI, just 3G .. Anyways, superb blog!
I am in fact glad to read this web site posts which includes lots of helpful
facts, thanks for providing such information.
Hello would you mind letting me know which web host you’re using?
I’ve loaded your blog in 3 completely different browsers and I must say this blog
loads a lot quicker then most. Can you suggest
a good internet hosting provider at a fair price?
Many thanks, I appreciate it!