Table of Contents
ToggleTOPIC 1: COORDINATE GEOMETRY ~ MATHEMATICS FORM 4
TOPIC 1: COORDINATE GEOMETRY ~ MATHEMATICS FORM 4
Equation of a Line
The General Equation of a Straight Line
Derive the general equation of a straight line
COORDINATES OF A POINT
•The coordinates of a points – are the values of x and y enclosed by the brackets which are used to describe the position of point in a line in the plane.
The plane is called xy-plane and it has two axis.
- horizontal axis known as axis and
- vertical axis known as axis
Consider the xy-plane below
The coordinates of points A, B, C ,D and E are A(2, 3), B(4, 4), C(-3, -1), D(2, -4) and E(1, 0).
Definition

Example 1
Find the gradient of the lines joining
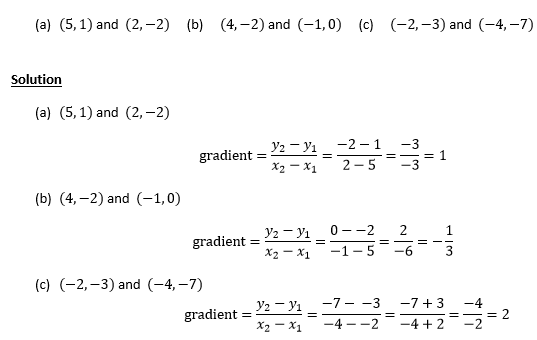
Example 2
(a) The line joining (2, -3) and (k, 5) has a gradient -2. Find k

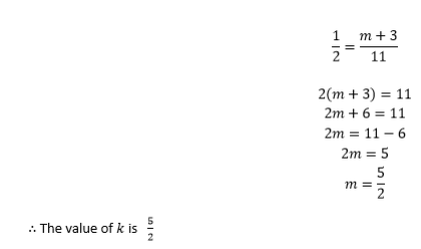
Exercise 1
1. Find the gradientof the line which passes through the following points ;
- (3,6) and (-2,8)
- (0,6) and (99,-12)
- (4,5)and (5,4)
2. A line passes through (3, a) and (4, -2), what is the value of a if the slope of the line is 4?
3. The gradient of the linewhich goes through (4,3) and (-5,k) is 2. Find the value of k.
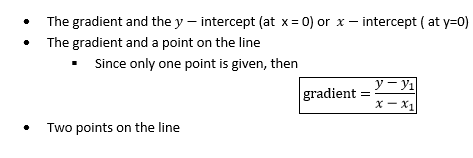
FINDING THE EQUATION OF A STRAIGHT LINE
The equation of a straight line can be determined if one of the following is given:-
Example 3
Find the equation of the line with the following
- Gradient 2 and intercept
- Gradient and passing through the point
- Passing through the points and
Solution


EQUATION OF A STRAIGHT LINE IN DIFFERENT FORMS
The equation of a line can be expressed in two forms

Example 4
INTERCEPTS

Therefore

Example 5
Find the y-intercept of the following lines

Example 6
Find the x and y-intercept of the following lines


Exercise 2
Attempt the following Questions.
- Find the y-intercept of the line 3x+2y = 18 .
- What is the x-intercept of the line passing through (3,3) and (-4,9)?
- Calculate the slope of the line given by the equation x-3y= 9
- Find the equation of the straight line with a slope -4 and passing through the point (0,0).
- Find the equation of the straight line with y-intercept 5 and passing through the point (-4,8).
GRAPHS OF STRAIGHT LINES
The graph of straight line can be drawn by using the following methods;
- By using intercepts
- By using the table of values
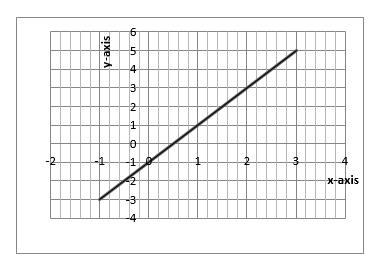
Example 7
Sketch the graph of Y = 2X – 1

SOLVING SIMULTANEOUS EQUATION BY GRAPHICAL METHOD
- Use the intercepts to plot the straight lines of the simultaneous equations
- The point where the two lines cross each other is the solution to the simultaneous equations
Example 8
Solve the following simultaneous equations by graphical method

Exercise 3
1. Draw the line 4x-2y=7 and 3x+y=7 on the same axis and hence determine their intersection point
2. Find the solutionfor each pair the following simultaneous equations by graphical method;
- y-x = 3 and 2x+y = 9
- 3x- 4y=-1 and x+y = 2
- x = 8 and 2x-3y = 10
Midpoint of a Line Segment
The Coordinates of the Midpoint of a Line Segment
Determine the coordinates of the midpoint of a line segment
Let S be a point with coordinates (x1,y1), T with coordinates (x2,y2) and M with coordinates (x,y) where M is the mid-point of ST. Consider the figure below:
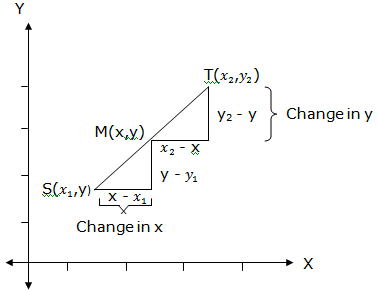
Considering the angles of the triangles SMC and TMD, the triangles SMC and TMD are similar since their equiangular

Example 9
Find the coordinates of the mid-point joining the points (-2,8) and (-4,-2)
Solution
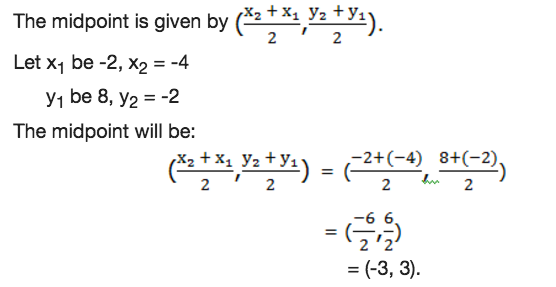
Therefore the coordinates of the midpoint of the line joining the points (-2,8) and (-4, -2) is (-3,3).
Distance Between Two Points on a Plane
The Distance Between Two Points on a Plane
Calculate the distance between two points on a plane
Consider two points, A(x1,y1) and B(x2,y2) as shown in the figure below:
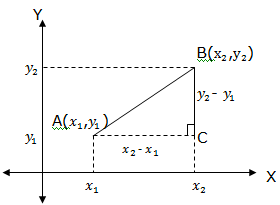
The distance between A and B in terms of x1, y1,x2, and y2can be found as follows:Join AB and draw doted lines as shown in the figure above.
Then, AC = x2– x1and BC = y2– y1
Since the triangle ABC is a right angled, then by applying Pythagoras theorem to the triangle ABC we obtain

Therefore the distance is 13 units.
Parallel and Perpendicular Lines
Gradients in order to Determine the Conditions for any Two Lines to be Parallel
Compute gradients in order to determine the conditions for any two lines to be parallel
The two lines which never meet when produced infinitely are called parallel lines. See figure below:
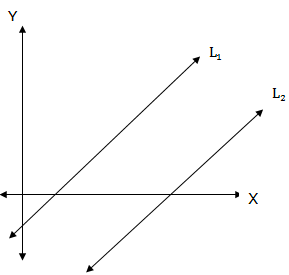
The two parallel lines must have the same slope. That is, if M1is the slope for L1and M2is the slope for L2thenM1= M2
Gradients in order to Determine the Conditions for any Two Lines to be Perpendicular
Compute gradients in order to determine the conditions for any two lines to be perpendicular
When two straight lines intersect at right angle, we say that the lines are perpendicular lines. See an illustration below.
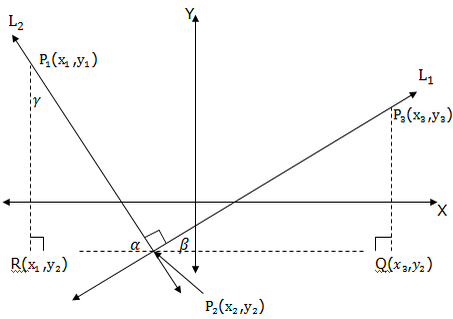
Consider the points P1(x1,y1), P2(x2,y2), P3(x3,y3), R(x1,y2) and Q(x3,y2) and the anglesα,β,γ(alpha, beta and gamma respectively).
- α+β = 90 (complementary angles)
- α+γ= 90 (complementary angles)
- β = γ (alternate interior angles)
Therefore the triangle P2QP3is similar to triangle P1RP2.
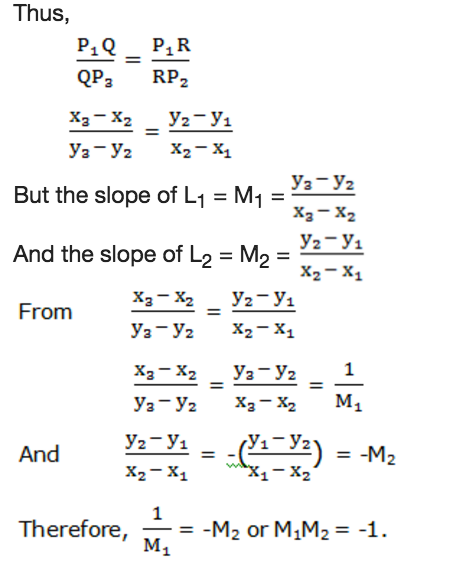
Generally two perpendicular lines L1and L2with slopes M1and M2respectively the product of their slopes is equal to negative one. That is M1M2= -1.
Example 10
Show that A(-3,1), B(1,2), C(0,-1) and D(-4,-2) are vertices of a parallelogram.
Solution
Let us find the slope of the lines AB, DC, AD and BC

We
see that each two opposite sides of the parallelogram have equal slope.
This means that the two opposite sides are parallel to each other,
which is the distinctive feature of the parallelogram. Therefore the
given vertices are the vertices of a parallelogram.
see that each two opposite sides of the parallelogram have equal slope.
This means that the two opposite sides are parallel to each other,
which is the distinctive feature of the parallelogram. Therefore the
given vertices are the vertices of a parallelogram.
Problems on Parallel and Perpendicular Lines
Solve problems on parallel and perpendicular lines
Example 11
Show that A(-3,2), B(5,6) and C(7,2) are vertices of a right angled triangle.
Solution
Right
angled triangle has two sides that are perpendicular, they form 90°.We
know that the slope of the line is given by: slope = change in y/change
in x
angled triangle has two sides that are perpendicular, they form 90°.We
know that the slope of the line is given by: slope = change in y/change
in x
Now,
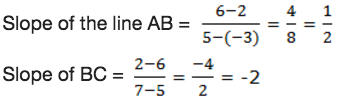
Since the slope of AB and BC are negative reciprocals, then the triangle ABC is a right angled triangle at B.



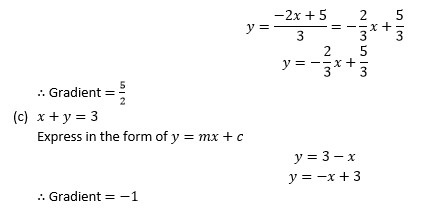
Hi there! I realize this is kind of off-topic however I needed to ask.
Does running a well-established blog such as yours take a large amount of work?
I’m completely new to running a blog but I do write
in my diary daily. I’d like to start a blog so I will be able to share my personal experience and thoughts online.
Please let me know if you have any kind of ideas or tips for brand
new aspiring blog owners. Thankyou!
Excellent write-up. I absolutely love this site. Stick with it!
This site was… how do you say it? Relevant!!
Finally I have found something which helped me.
Many thanks!
Have you ever thought about writing an e-book or guest authoring
on other sites? I have a blog centered on the same information you discuss
and would love to have you share some stories/information. I know my readers would enjoy your work.
If you’re even remotely interested, feel free to send me an e mail.
Ahaa, its good dialogue concerning this post at this place at this webpage, I have read all that, so now me also commenting
here.
When I initially left a comment I appear to have clicked on the -Notify me when new comments are added- checkbox and
now whenever a comment is added I recieve four emails with the same comment.
Perhaps there is a means you are able to remove me from that service?
Thank you!
Its such as you learn my thoughts! You appear to understand so much approximately this, like you wrote the book in it or something.
I believe that you can do with a few percent to power the
message home a little bit, however instead of that, that is great blog.
A great read. I will certainly be back.
Fantastic beat ! I wish to apprentice even as you
amend your website, how can i subscribe for a blog web site?
The account aided me a applicable deal. I had been tiny bit familiar of this your
broadcast offered bright transparent idea
We’re a group of volunteers and starting a new scheme in our community.
Your website provided us with valuable info to work on. You’ve
done an impressive job and our entire community will be
thankful to you.
Thank you a bunch for sharing this with all people you really recognise what you’re speaking about!
Bookmarked. Please also discuss with my website =). We could have a
hyperlink alternate agreement among us
I’m not sure exactly why but this weblog is loading very
slow for me. Is anyone else having this issue or is it a issue on my end?
I’ll check back later and see if the problem still exists.
Every weekend i used to visit this site, because i wish for
enjoyment, as this this web page conations actually pleasant funny
material too.
Thanks , I have recently been looking for info about this subject for a while and yours is the greatest I have found out so far.
However, what in regards to the conclusion? Are you
positive concerning the supply?
Just wish to say your article is as surprising.
The clearness in your post is simply nice and i can assume you’re
an expert on this subject. Fine with your permission let me to grab
your RSS feed to keep up to date with forthcoming post.
Thanks a million and please continue the gratifying work.
Hello there! Would you mind if I share your
blog with my zynga group? There’s a lot of people that I think would really appreciate
your content. Please let me know. Thank you
Ahaa, its good conversation concerning this post at this place at this web site, I
have read all that, so now me also commenting here.
Somebody necessarily help to make significantly articles I might state.
This is the first time I frequented your website page
and to this point? I surprised with the research you made to create this actual post incredible.
Great process!
Marvelous, what a webpage it is! This website provides valuable facts to us, keep
it up.
Hey there would you mind sharing which blog platform you’re
working with? I’m looking to start my own blog soon but I’m having a tough time deciding between BlogEngine/Wordpress/B2evolution and Drupal.
The reason I ask is because your layout seems different
then most blogs and I’m looking for something unique.
P.S Sorry for being off-topic but I had to ask!
Informative article, totally what I needed.
Hi there i am kavin, its my first time to commenting anywhere,
when i read this paragraph i thought i could also make comment due to this sensible post.
Pretty section of content. I simply stumbled upon your web site and in accession capital to say that I acquire actually enjoyed account your blog posts.
Any way I will be subscribing to your feeds and even I success you get admission to constantly fast.
You ought to take part in a contest for one of the greatest sites
on the net. I most certainly will recommend
this website!
This paragraph presents clear idea for the new people
of blogging, that actually how to do blogging and site-building.
After looking over a few of the articles on your web site, I truly
like your technique of blogging. I book-marked it to my bookmark
site list and will be checking back in the near future. Please visit my web site as well and let me know
your opinion.