Table of Contents
ToggleTOPIC 1: COORDINATE GEOMETRY ~ MATHEMATICS FORM 4
TOPIC 1: COORDINATE GEOMETRY ~ MATHEMATICS FORM 4
Equation of a Line
The General Equation of a Straight Line
Derive the general equation of a straight line
COORDINATES OF A POINT
•The coordinates of a points – are the values of x and y enclosed by the brackets which are used to describe the position of point in a line in the plane.
The plane is called xy-plane and it has two axis.
- horizontal axis known as axis and
- vertical axis known as axis
Consider the xy-plane below
The coordinates of points A, B, C ,D and E are A(2, 3), B(4, 4), C(-3, -1), D(2, -4) and E(1, 0).
Definition

Example 1
Find the gradient of the lines joining
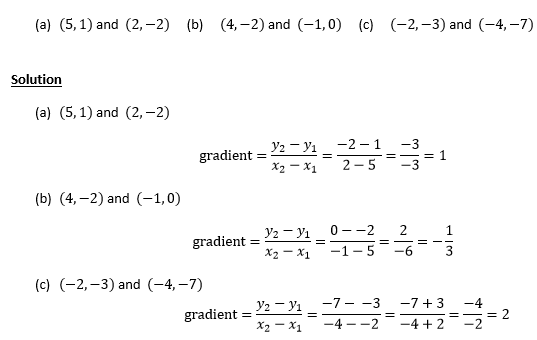
Example 2
(a) The line joining (2, -3) and (k, 5) has a gradient -2. Find k

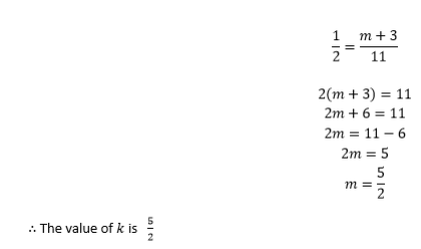
Exercise 1
1. Find the gradientof the line which passes through the following points ;
- (3,6) and (-2,8)
- (0,6) and (99,-12)
- (4,5)and (5,4)
2. A line passes through (3, a) and (4, -2), what is the value of a if the slope of the line is 4?
3. The gradient of the linewhich goes through (4,3) and (-5,k) is 2. Find the value of k.
FINDING THE EQUATION OF A STRAIGHT LINE
The equation of a straight line can be determined if one of the following is given:-
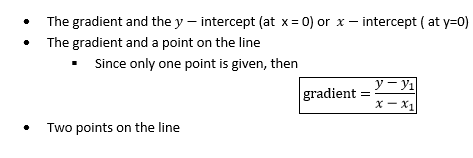
Example 3
Find the equation of the line with the following
- Gradient 2 and intercept
- Gradient and passing through the point
- Passing through the points and
Solution


EQUATION OF A STRAIGHT LINE IN DIFFERENT FORMS
The equation of a line can be expressed in two forms

Example 4
INTERCEPTS

Therefore

Example 5
Find the y-intercept of the following lines

Example 6
Find the x and y-intercept of the following lines


Exercise 2
Attempt the following Questions.
- Find the y-intercept of the line 3x+2y = 18 .
- What is the x-intercept of the line passing through (3,3) and (-4,9)?
- Calculate the slope of the line given by the equation x-3y= 9
- Find the equation of the straight line with a slope -4 and passing through the point (0,0).
- Find the equation of the straight line with y-intercept 5 and passing through the point (-4,8).
GRAPHS OF STRAIGHT LINES
The graph of straight line can be drawn by using the following methods;
- By using intercepts
- By using the table of values
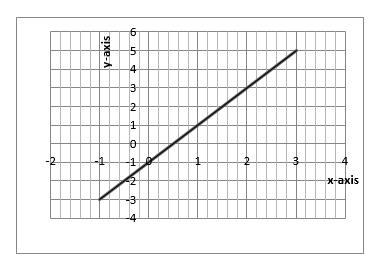
Example 7
Sketch the graph of Y = 2X – 1

SOLVING SIMULTANEOUS EQUATION BY GRAPHICAL METHOD
- Use the intercepts to plot the straight lines of the simultaneous equations
- The point where the two lines cross each other is the solution to the simultaneous equations
Example 8
Solve the following simultaneous equations by graphical method

Exercise 3
1. Draw the line 4x-2y=7 and 3x+y=7 on the same axis and hence determine their intersection point
2. Find the solutionfor each pair the following simultaneous equations by graphical method;
- y-x = 3 and 2x+y = 9
- 3x- 4y=-1 and x+y = 2
- x = 8 and 2x-3y = 10
Midpoint of a Line Segment
The Coordinates of the Midpoint of a Line Segment
Determine the coordinates of the midpoint of a line segment
Let S be a point with coordinates (x1,y1), T with coordinates (x2,y2) and M with coordinates (x,y) where M is the mid-point of ST. Consider the figure below:
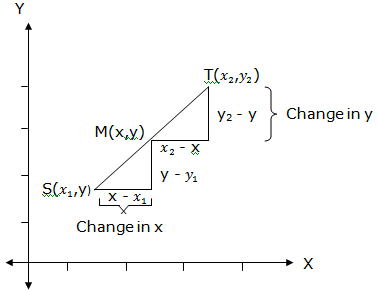
Considering the angles of the triangles SMC and TMD, the triangles SMC and TMD are similar since their equiangular

Example 9
Find the coordinates of the mid-point joining the points (-2,8) and (-4,-2)
Solution
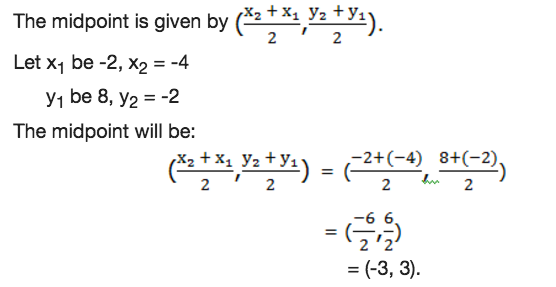
Therefore the coordinates of the midpoint of the line joining the points (-2,8) and (-4, -2) is (-3,3).
Distance Between Two Points on a Plane
The Distance Between Two Points on a Plane
Calculate the distance between two points on a plane
Consider two points, A(x1,y1) and B(x2,y2) as shown in the figure below:
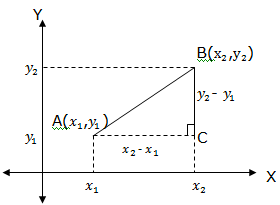
The distance between A and B in terms of x1, y1,x2, and y2can be found as follows:Join AB and draw doted lines as shown in the figure above.
Then, AC = x2– x1and BC = y2– y1
Since the triangle ABC is a right angled, then by applying Pythagoras theorem to the triangle ABC we obtain

Therefore the distance is 13 units.
Parallel and Perpendicular Lines
Gradients in order to Determine the Conditions for any Two Lines to be Parallel
Compute gradients in order to determine the conditions for any two lines to be parallel
The two lines which never meet when produced infinitely are called parallel lines. See figure below:
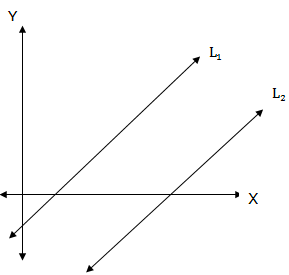
The two parallel lines must have the same slope. That is, if M1is the slope for L1and M2is the slope for L2thenM1= M2
Gradients in order to Determine the Conditions for any Two Lines to be Perpendicular
Compute gradients in order to determine the conditions for any two lines to be perpendicular
When two straight lines intersect at right angle, we say that the lines are perpendicular lines. See an illustration below.
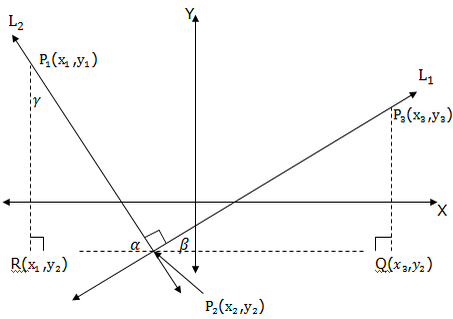
Consider the points P1(x1,y1), P2(x2,y2), P3(x3,y3), R(x1,y2) and Q(x3,y2) and the anglesα,β,γ(alpha, beta and gamma respectively).
- α+β = 90 (complementary angles)
- α+γ= 90 (complementary angles)
- β = γ (alternate interior angles)
Therefore the triangle P2QP3is similar to triangle P1RP2.
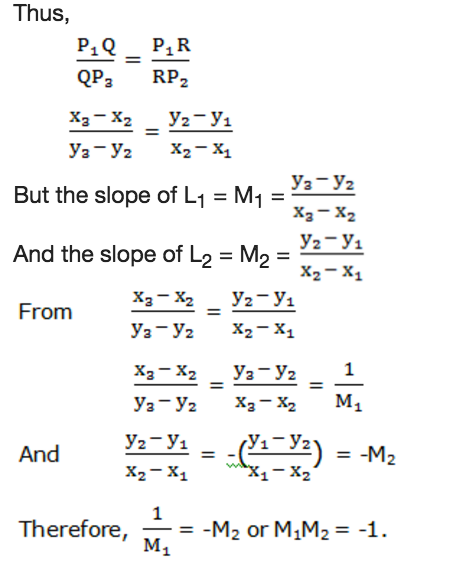
Generally two perpendicular lines L1and L2with slopes M1and M2respectively the product of their slopes is equal to negative one. That is M1M2= -1.
Example 10
Show that A(-3,1), B(1,2), C(0,-1) and D(-4,-2) are vertices of a parallelogram.
Solution
Let us find the slope of the lines AB, DC, AD and BC

We
see that each two opposite sides of the parallelogram have equal slope.
This means that the two opposite sides are parallel to each other,
which is the distinctive feature of the parallelogram. Therefore the
given vertices are the vertices of a parallelogram.
see that each two opposite sides of the parallelogram have equal slope.
This means that the two opposite sides are parallel to each other,
which is the distinctive feature of the parallelogram. Therefore the
given vertices are the vertices of a parallelogram.
Problems on Parallel and Perpendicular Lines
Solve problems on parallel and perpendicular lines
Example 11
Show that A(-3,2), B(5,6) and C(7,2) are vertices of a right angled triangle.
Solution
Right
angled triangle has two sides that are perpendicular, they form 90°.We
know that the slope of the line is given by: slope = change in y/change
in x
angled triangle has two sides that are perpendicular, they form 90°.We
know that the slope of the line is given by: slope = change in y/change
in x
Now,
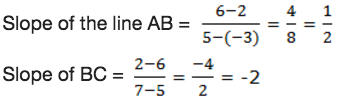
Since the slope of AB and BC are negative reciprocals, then the triangle ABC is a right angled triangle at B.



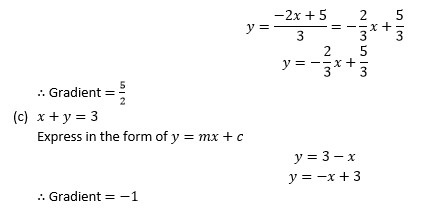
You are so interesting! I do not suppose I have read through something like
this before. So good to find someone with some genuine thoughts on this topic.
Seriously.. many thanks for starting this up. This website is one
thing that is needed on the internet, someone with a little originality!
I think this is one of the most important info for me.
And i am glad reading your article. But should remark on few general things,
The site style is ideal, the articles is really excellent :
D. Good job, cheers
Wow that was strange. I just wrote an extremely long comment but after I clicked submit my comment didn’t appear.
Grrrr… well I’m not writing all that over again. Anyway,
just wanted to say excellent blog!
If you would like to obtain a great deal from this post then you have to apply such strategies to your won website.
Hello everyone, it’s my first pay a quick visit at this web page, and article is in fact fruitful designed for me, keep up posting such articles or reviews.
Hmm is anyone else experiencing problems with the pictures on this blog
loading? I’m trying to find out if its a problem on my end or if it’s the blog.
Any feedback would be greatly appreciated.
Very good write-up. I definitely appreciate this site.
Keep writing!
Does your blog have a contact page? I’m having trouble
locating it but, I’d like to shoot you an e-mail.
I’ve got some ideas for your blog you might be interested in hearing.
Either way, great website and I look forward
to seeing it develop over time.
Its like you read my mind! You seem to know
so much about this, like you wrote the book in it or something.
I think that you could do with some pics to drive the message home a bit, but instead
of that, this is magnificent blog. A great read.
I will certainly be back.
Heya i am for the first time here. I found this board and I in finding It truly helpful & it helped me out
much. I am hoping to offer something back and help others such as
you aided me.
Wonderful beat ! I wish to apprentice while
you amend your web site, how could i subscribe for a weblog web
site? The account aided me a acceptable deal. I had been tiny bit familiar of this your broadcast provided brilliant clear idea
Since the admin of this website is working, no uncertainty very rapidly it will be famous, due to its feature contents.
Hi there! This article couldn’t be written much better! Looking through this article reminds me of my previous roommate!
He always kept preaching about this. I am going to send this post to him.
Fairly certain he will have a good read. Thank you for sharing!
I for all time emailed this web site post page to all my associates, because if like to read it after that my links will too.
I like the valuable info you provide in your articles.
I’ll bookmark your weblog and check again here frequently.
I’m quite sure I’ll learn many new stuff right here! Best of
luck for the next!
I was wondering if you ever considered changing the structure
of your website? Its very well written; I love what youve
got to say. But maybe you could a little more in the way of content so
people could connect with it better. Youve got an awful
lot of text for only having 1 or 2 pictures. Maybe you could space it out
better?
I just like the helpful information you supply to your articles.
I will bookmark your weblog and check once more here regularly.
I’m quite sure I will learn lots of new stuff right right here!
Best of luck for the next!
Howdy! Do you know if they make any plugins to safeguard against hackers?
I’m kinda paranoid about losing everything I’ve worked hard on. Any recommendations?
My family every time say that I am wasting my time here at net, however I know I am getting experience daily by reading such good
posts.
I do not know whether it’s just me or if perhaps everyone else experiencing issues with your blog.
It looks like some of the text in your posts are
running off the screen. Can someone else please comment and let me know if this is happening to them
as well? This may be a problem with my web browser because I’ve had
this happen before. Many thanks
I loved as much as you’ll receive carried out right here.
The sketch is tasteful, your authored subject matter stylish.
nonetheless, you command get got an shakiness over
that you wish be delivering the following. unwell unquestionably come more formerly again since exactly the same
nearly a lot often inside case you shield this hike.
Hi there, I log on to your blog on a regular basis. Your
humoristic style is awesome, keep doing what you’re
doing!
I blog often and I seriously thank you for your information. The article has
truly peaked my interest. I’m going to book mark your website and keep checking for new
details about once per week. I subscribed to your RSS feed too.
What i don’t understood is actually how you’re now not actually a lot more
well-appreciated than you may be now. You’re so intelligent.
You know thus significantly when it comes to this subject, made me in my opinion imagine it from a lot
of varied angles. Its like men and women are not interested unless it’s one thing to accomplish with Woman gaga!
Your individual stuffs outstanding. At all times maintain it up!
Good day! I could have sworn I’ve been to this site before but
after checking through some of the post I realized it’s new to
me. Nonetheless, I’m definitely happy I found it and I’ll be bookmarking and checking back often!