Table of Contents
ToggleTOPIC 1: COORDINATE GEOMETRY ~ MATHEMATICS FORM 4
TOPIC 1: COORDINATE GEOMETRY ~ MATHEMATICS FORM 4
Equation of a Line
The General Equation of a Straight Line
Derive the general equation of a straight line
COORDINATES OF A POINT
•The coordinates of a points – are the values of x and y enclosed by the brackets which are used to describe the position of point in a line in the plane.
The plane is called xy-plane and it has two axis.
- horizontal axis known as axis and
- vertical axis known as axis
Consider the xy-plane below
The coordinates of points A, B, C ,D and E are A(2, 3), B(4, 4), C(-3, -1), D(2, -4) and E(1, 0).
Definition

Example 1
Find the gradient of the lines joining
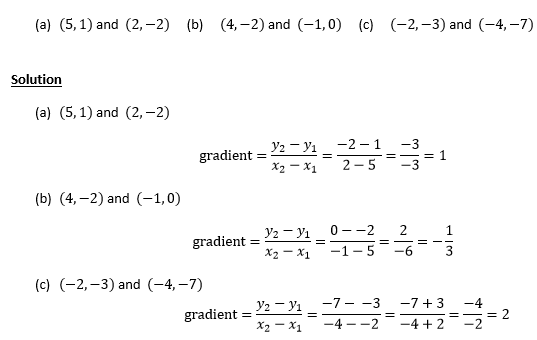
Example 2
(a) The line joining (2, -3) and (k, 5) has a gradient -2. Find k

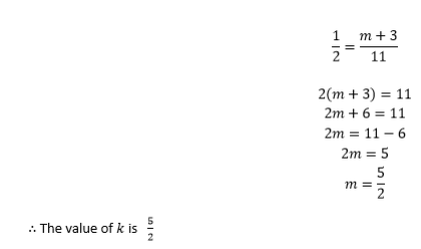
Exercise 1
1. Find the gradientof the line which passes through the following points ;
- (3,6) and (-2,8)
- (0,6) and (99,-12)
- (4,5)and (5,4)
2. A line passes through (3, a) and (4, -2), what is the value of a if the slope of the line is 4?
3. The gradient of the linewhich goes through (4,3) and (-5,k) is 2. Find the value of k.
FINDING THE EQUATION OF A STRAIGHT LINE
The equation of a straight line can be determined if one of the following is given:-
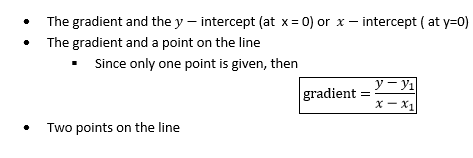
Example 3
Find the equation of the line with the following
- Gradient 2 and intercept
- Gradient and passing through the point
- Passing through the points and
Solution


EQUATION OF A STRAIGHT LINE IN DIFFERENT FORMS
The equation of a line can be expressed in two forms

Example 4
INTERCEPTS

Therefore

Example 5
Find the y-intercept of the following lines

Example 6
Find the x and y-intercept of the following lines


Exercise 2
Attempt the following Questions.
- Find the y-intercept of the line 3x+2y = 18 .
- What is the x-intercept of the line passing through (3,3) and (-4,9)?
- Calculate the slope of the line given by the equation x-3y= 9
- Find the equation of the straight line with a slope -4 and passing through the point (0,0).
- Find the equation of the straight line with y-intercept 5 and passing through the point (-4,8).
GRAPHS OF STRAIGHT LINES
The graph of straight line can be drawn by using the following methods;
- By using intercepts
- By using the table of values
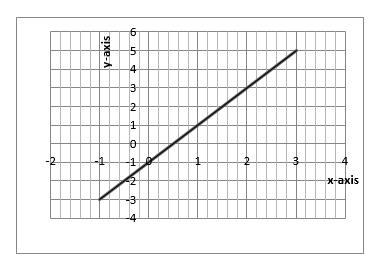
Example 7
Sketch the graph of Y = 2X – 1

SOLVING SIMULTANEOUS EQUATION BY GRAPHICAL METHOD
- Use the intercepts to plot the straight lines of the simultaneous equations
- The point where the two lines cross each other is the solution to the simultaneous equations
Example 8
Solve the following simultaneous equations by graphical method

Exercise 3
1. Draw the line 4x-2y=7 and 3x+y=7 on the same axis and hence determine their intersection point
2. Find the solutionfor each pair the following simultaneous equations by graphical method;
- y-x = 3 and 2x+y = 9
- 3x- 4y=-1 and x+y = 2
- x = 8 and 2x-3y = 10
Midpoint of a Line Segment
The Coordinates of the Midpoint of a Line Segment
Determine the coordinates of the midpoint of a line segment
Let S be a point with coordinates (x1,y1), T with coordinates (x2,y2) and M with coordinates (x,y) where M is the mid-point of ST. Consider the figure below:
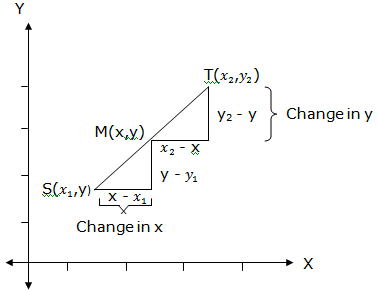
Considering the angles of the triangles SMC and TMD, the triangles SMC and TMD are similar since their equiangular

Example 9
Find the coordinates of the mid-point joining the points (-2,8) and (-4,-2)
Solution
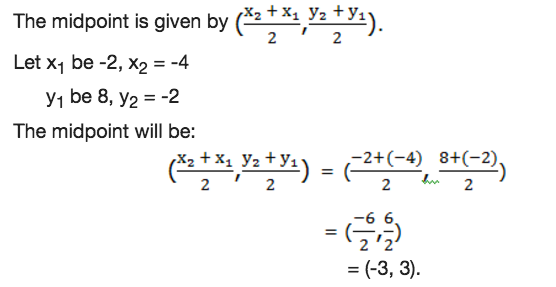
Therefore the coordinates of the midpoint of the line joining the points (-2,8) and (-4, -2) is (-3,3).
Distance Between Two Points on a Plane
The Distance Between Two Points on a Plane
Calculate the distance between two points on a plane
Consider two points, A(x1,y1) and B(x2,y2) as shown in the figure below:
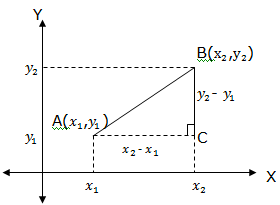
The distance between A and B in terms of x1, y1,x2, and y2can be found as follows:Join AB and draw doted lines as shown in the figure above.
Then, AC = x2– x1and BC = y2– y1
Since the triangle ABC is a right angled, then by applying Pythagoras theorem to the triangle ABC we obtain

Therefore the distance is 13 units.
Parallel and Perpendicular Lines
Gradients in order to Determine the Conditions for any Two Lines to be Parallel
Compute gradients in order to determine the conditions for any two lines to be parallel
The two lines which never meet when produced infinitely are called parallel lines. See figure below:
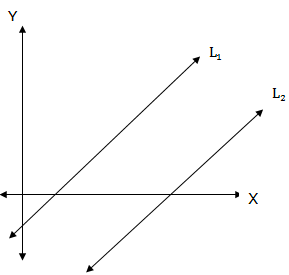
The two parallel lines must have the same slope. That is, if M1is the slope for L1and M2is the slope for L2thenM1= M2
Gradients in order to Determine the Conditions for any Two Lines to be Perpendicular
Compute gradients in order to determine the conditions for any two lines to be perpendicular
When two straight lines intersect at right angle, we say that the lines are perpendicular lines. See an illustration below.
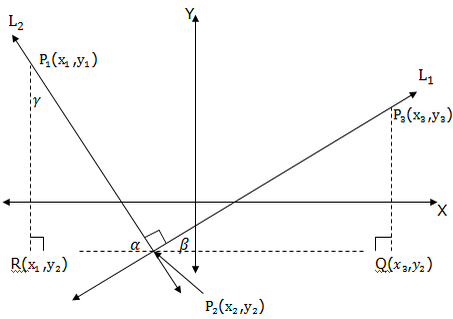
Consider the points P1(x1,y1), P2(x2,y2), P3(x3,y3), R(x1,y2) and Q(x3,y2) and the anglesα,β,γ(alpha, beta and gamma respectively).
- α+β = 90 (complementary angles)
- α+γ= 90 (complementary angles)
- β = γ (alternate interior angles)
Therefore the triangle P2QP3is similar to triangle P1RP2.
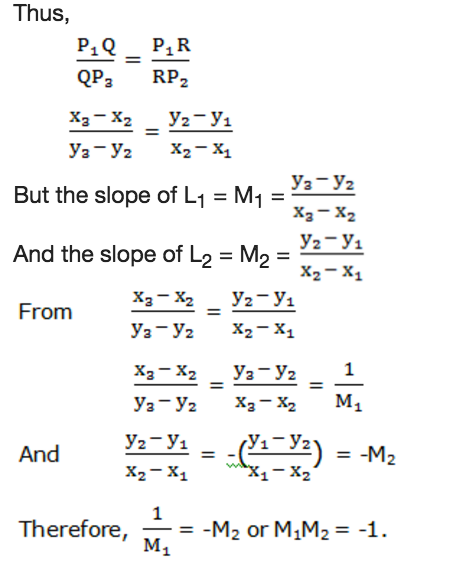
Generally two perpendicular lines L1and L2with slopes M1and M2respectively the product of their slopes is equal to negative one. That is M1M2= -1.
Example 10
Show that A(-3,1), B(1,2), C(0,-1) and D(-4,-2) are vertices of a parallelogram.
Solution
Let us find the slope of the lines AB, DC, AD and BC

We
see that each two opposite sides of the parallelogram have equal slope.
This means that the two opposite sides are parallel to each other,
which is the distinctive feature of the parallelogram. Therefore the
given vertices are the vertices of a parallelogram.
see that each two opposite sides of the parallelogram have equal slope.
This means that the two opposite sides are parallel to each other,
which is the distinctive feature of the parallelogram. Therefore the
given vertices are the vertices of a parallelogram.
Problems on Parallel and Perpendicular Lines
Solve problems on parallel and perpendicular lines
Example 11
Show that A(-3,2), B(5,6) and C(7,2) are vertices of a right angled triangle.
Solution
Right
angled triangle has two sides that are perpendicular, they form 90°.We
know that the slope of the line is given by: slope = change in y/change
in x
angled triangle has two sides that are perpendicular, they form 90°.We
know that the slope of the line is given by: slope = change in y/change
in x
Now,
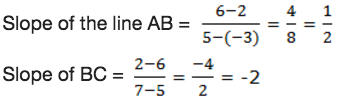
Since the slope of AB and BC are negative reciprocals, then the triangle ABC is a right angled triangle at B.



Hiya! Quick question that’s entirely off topic. Do you know how to
make your site mobile friendly? My weblog looks weird
when viewing from my iphone. I’m trying to find a theme or plugin that might be able to resolve this
problem. If you have any recommendations, please share. Many thanks!
Hi I am so excited I found your site, I really found you by accident,
while I was looking on Digg for something else, Regardless
I am here now and would just like to say cheers for a tremendous post and a all round interesting blog (I also love
the theme/design), I don’t have time to browse it all at
the moment but I have bookmarked it and also added in your
RSS feeds, so when I have time I will be back to read a lot more, Please do keep up the excellent b.
Hey There. I found your blog using msn. This is an extremely well written article.
I will make sure to bookmark it and come back to read more of your useful information.
Thanks for the post. I’ll definitely comeback.
Thanks a lot for sharing this with all people you
really realize what you’re talking about! Bookmarked.
Please additionally consult with my website =). We may have a link exchange agreement among us
Great items from you, man. I have remember your stuff previous to and you are just too magnificent.
I actually like what you’ve acquired here, really like what you’re saying and
the best way through which you assert it.
You’re making it entertaining and you continue to take care of to keep it wise.
I cant wait to learn much more from you. That is actually a tremendous website.
I all the time emailed this webpage post page to all my
friends, for the reason that if like to read it afterward my friends will too.
I’m amazed, I must say. Seldom do I encounter a blog that’s both educative and engaging, and
let me tell you, you’ve hit the nail on the head. The issue is something not enough people are
speaking intelligently about. I’m very happy I stumbled across this during my search for something concerning this.
Hi it’s me, I am also visiting this site on a regular basis,
this web page is truly pleasant and the viewers are really sharing nice thoughts.
You made some decent points there. I looked on the web for more info about
the issue and found most individuals will go along with your views on this site.
This is a topic that’s close to my heart… Best wishes!
Where are your contact details though?
I like the valuable info you supply to your articles. I’ll bookmark your weblog and take a look
at once more right here regularly. I’m slightly
sure I’ll learn plenty of new stuff proper here!
Good luck for the following!
It’s remarkable in favor of me to have a web site, which is beneficial for
my know-how. thanks admin
This post is invaluable. Where can I find out more?
I read this piece of writing completely regarding the comparison of newest and earlier technologies, it’s remarkable article.
Thank you a lot for sharing this with all of us you really realize what you are talking approximately!
Bookmarked. Please also seek advice from my website =).
We could have a link trade agreement between us
This paragraph gives clear idea in support of the new viewers of blogging, that really how to do blogging and site-building.
WOW just what I was looking for. Came here by searching for Sa Gaming
Saved as a favorite, I love your site!
I visit day-to-day some blogs and websites to read posts,
however this weblog presents feature based posts.
Thanks to my father who stated to me concerning this weblog, this website
is actually awesome.
I really like your blog.. very nice colors & theme.
Did you make this website yourself or did you hire someone to do it for
you? Plz reply as I’m looking to create my own blog and would like to find out where u got this from.
many thanks
Pretty section of content. I just stumbled upon your site and in accession capital to assert that I acquire in fact enjoyed account
your blog posts. Anyway I will be subscribing to your augment and even I achievement you access consistently rapidly.
It’s in reality a great and helpful piece of info. I’m glad that you just shared
this helpful info with us. Please stay us up to date like this.
Thank you for sharing.
I don’t know if it’s just me or if everybody else experiencing issues with your website.
It appears like some of the written text on your posts are running off
the screen. Can someone else please provide feedback and let me know if this is happening to them as
well? This might be a issue with my browser because I’ve had
this happen previously. Cheers
Pretty nice post. I just stumbled upon your weblog and
wanted to say that I have really enjoyed surfing around your blog posts.
In any case I’ll be subscribing to your rss feed and I hope you
write again very soon!