Table of Contents
ToggleTOPIC 1: COORDINATE GEOMETRY ~ MATHEMATICS FORM 4
TOPIC 1: COORDINATE GEOMETRY ~ MATHEMATICS FORM 4
Equation of a Line
The General Equation of a Straight Line
Derive the general equation of a straight line
COORDINATES OF A POINT
•The coordinates of a points – are the values of x and y enclosed by the brackets which are used to describe the position of point in a line in the plane.
The plane is called xy-plane and it has two axis.
- horizontal axis known as axis and
- vertical axis known as axis
Consider the xy-plane below
The coordinates of points A, B, C ,D and E are A(2, 3), B(4, 4), C(-3, -1), D(2, -4) and E(1, 0).
Definition

Example 1
Find the gradient of the lines joining
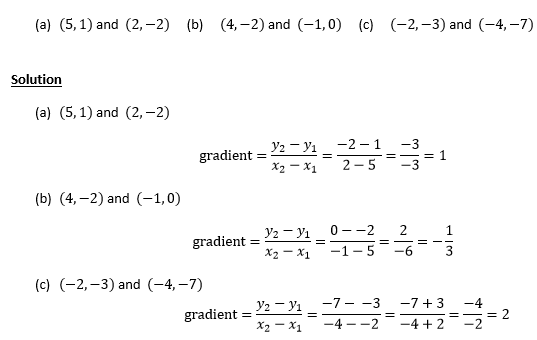
Example 2
(a) The line joining (2, -3) and (k, 5) has a gradient -2. Find k

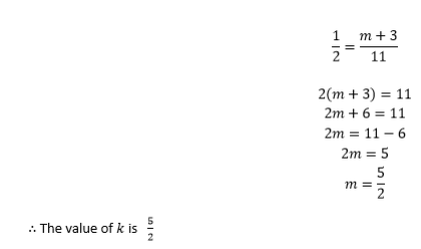
Exercise 1
1. Find the gradientof the line which passes through the following points ;
- (3,6) and (-2,8)
- (0,6) and (99,-12)
- (4,5)and (5,4)
2. A line passes through (3, a) and (4, -2), what is the value of a if the slope of the line is 4?
3. The gradient of the linewhich goes through (4,3) and (-5,k) is 2. Find the value of k.
FINDING THE EQUATION OF A STRAIGHT LINE
The equation of a straight line can be determined if one of the following is given:-
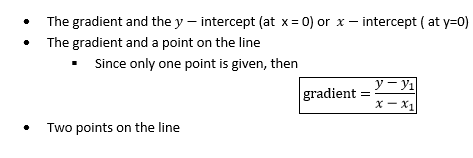
Example 3
Find the equation of the line with the following
- Gradient 2 and intercept
- Gradient and passing through the point
- Passing through the points and
Solution


EQUATION OF A STRAIGHT LINE IN DIFFERENT FORMS
The equation of a line can be expressed in two forms

Example 4
INTERCEPTS

Therefore

Example 5
Find the y-intercept of the following lines

Example 6
Find the x and y-intercept of the following lines


Exercise 2
Attempt the following Questions.
- Find the y-intercept of the line 3x+2y = 18 .
- What is the x-intercept of the line passing through (3,3) and (-4,9)?
- Calculate the slope of the line given by the equation x-3y= 9
- Find the equation of the straight line with a slope -4 and passing through the point (0,0).
- Find the equation of the straight line with y-intercept 5 and passing through the point (-4,8).
GRAPHS OF STRAIGHT LINES
The graph of straight line can be drawn by using the following methods;
- By using intercepts
- By using the table of values
Example 7
Sketch the graph of Y = 2X – 1

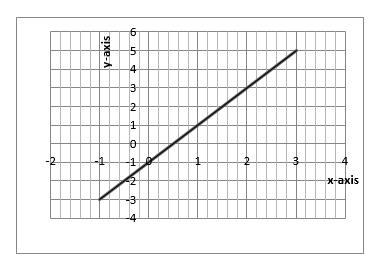
SOLVING SIMULTANEOUS EQUATION BY GRAPHICAL METHOD
- Use the intercepts to plot the straight lines of the simultaneous equations
- The point where the two lines cross each other is the solution to the simultaneous equations
Example 8
Solve the following simultaneous equations by graphical method

Exercise 3
1. Draw the line 4x-2y=7 and 3x+y=7 on the same axis and hence determine their intersection point
2. Find the solutionfor each pair the following simultaneous equations by graphical method;
- y-x = 3 and 2x+y = 9
- 3x- 4y=-1 and x+y = 2
- x = 8 and 2x-3y = 10
Midpoint of a Line Segment
The Coordinates of the Midpoint of a Line Segment
Determine the coordinates of the midpoint of a line segment
Let S be a point with coordinates (x1,y1), T with coordinates (x2,y2) and M with coordinates (x,y) where M is the mid-point of ST. Consider the figure below:
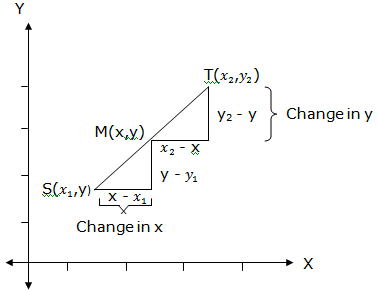
Considering the angles of the triangles SMC and TMD, the triangles SMC and TMD are similar since their equiangular

Example 9
Find the coordinates of the mid-point joining the points (-2,8) and (-4,-2)
Solution
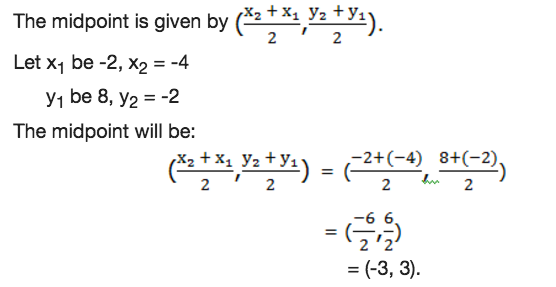
Therefore the coordinates of the midpoint of the line joining the points (-2,8) and (-4, -2) is (-3,3).
Distance Between Two Points on a Plane
The Distance Between Two Points on a Plane
Calculate the distance between two points on a plane
Consider two points, A(x1,y1) and B(x2,y2) as shown in the figure below:
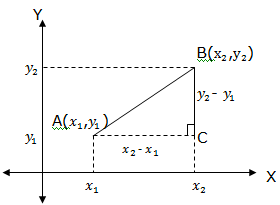
The distance between A and B in terms of x1, y1,x2, and y2can be found as follows:Join AB and draw doted lines as shown in the figure above.
Then, AC = x2– x1and BC = y2– y1
Since the triangle ABC is a right angled, then by applying Pythagoras theorem to the triangle ABC we obtain

Therefore the distance is 13 units.
Parallel and Perpendicular Lines
Gradients in order to Determine the Conditions for any Two Lines to be Parallel
Compute gradients in order to determine the conditions for any two lines to be parallel
The two lines which never meet when produced infinitely are called parallel lines. See figure below:
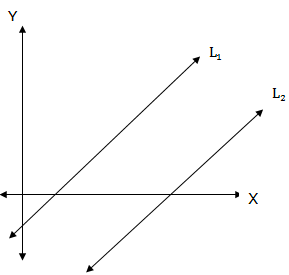
The two parallel lines must have the same slope. That is, if M1is the slope for L1and M2is the slope for L2thenM1= M2
Gradients in order to Determine the Conditions for any Two Lines to be Perpendicular
Compute gradients in order to determine the conditions for any two lines to be perpendicular
When two straight lines intersect at right angle, we say that the lines are perpendicular lines. See an illustration below.
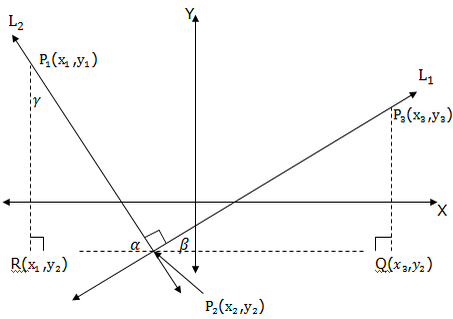
Consider the points P1(x1,y1), P2(x2,y2), P3(x3,y3), R(x1,y2) and Q(x3,y2) and the anglesα,β,γ(alpha, beta and gamma respectively).
- α+β = 90 (complementary angles)
- α+γ= 90 (complementary angles)
- β = γ (alternate interior angles)
Therefore the triangle P2QP3is similar to triangle P1RP2.
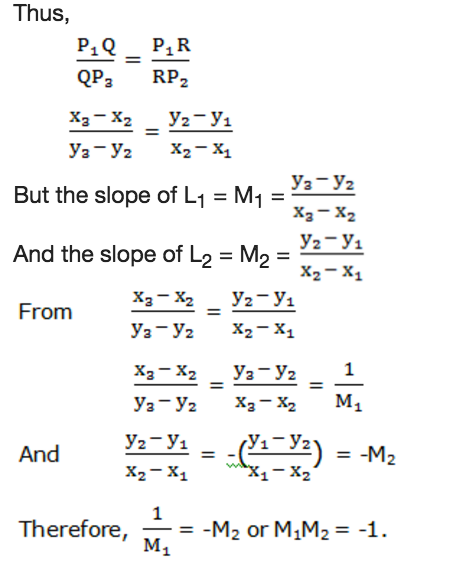
Generally two perpendicular lines L1and L2with slopes M1and M2respectively the product of their slopes is equal to negative one. That is M1M2= -1.
Example 10
Show that A(-3,1), B(1,2), C(0,-1) and D(-4,-2) are vertices of a parallelogram.
Solution
Let us find the slope of the lines AB, DC, AD and BC

We
see that each two opposite sides of the parallelogram have equal slope.
This means that the two opposite sides are parallel to each other,
which is the distinctive feature of the parallelogram. Therefore the
given vertices are the vertices of a parallelogram.
see that each two opposite sides of the parallelogram have equal slope.
This means that the two opposite sides are parallel to each other,
which is the distinctive feature of the parallelogram. Therefore the
given vertices are the vertices of a parallelogram.
Problems on Parallel and Perpendicular Lines
Solve problems on parallel and perpendicular lines
Example 11
Show that A(-3,2), B(5,6) and C(7,2) are vertices of a right angled triangle.
Solution
Right
angled triangle has two sides that are perpendicular, they form 90°.We
know that the slope of the line is given by: slope = change in y/change
in x
angled triangle has two sides that are perpendicular, they form 90°.We
know that the slope of the line is given by: slope = change in y/change
in x
Now,
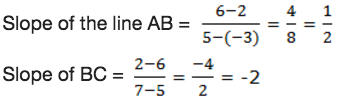
Since the slope of AB and BC are negative reciprocals, then the triangle ABC is a right angled triangle at B.



Everything is very open with a very clear description of the issues.
It was definitely informative. Your website is extremely helpful.
Thanks for sharing!
I’ve learn several just right stuff here. Certainly price bookmarking for revisiting.
I surprise how much effort you set to create this sort of great informative website.
I’d like to thank you for the efforts you have put in writing
this site. I am hoping to see the same high-grade blog posts by you later on as well.
In truth, your creative writing abilities has
inspired me to get my own, personal website
now 😉
Hi! I understand this is kind of off-topic but I needed to ask.
Does operating a well-established blog such as yours require a large amount of work?
I’m completely new to blogging however I do write in my journal everyday.
I’d like to start a blog so I can easily share my personal experience and
feelings online. Please let me know if you have any kind of
recommendations or tips for brand new aspiring blog owners.
Appreciate it!
Hi there mates, how is the whole thing, and what you would like to say regarding this piece of
writing, in my view its truly awesome in support of me.
Hey There. I found your blog using msn. This is a very well written article.
I’ll be sure to bookmark it and come back to read more of your useful info.
Thanks for the post. I will definitely return.
Can you tell us more about this? I’d care to find out more details.
Good web site you have here.. It’s difficult to find high quality
writing like yours these days. I honestly appreciate individuals like
you! Take care!!
Highly descriptive article, I liked that a lot. Will there be a part 2?
I blog frequently and I seriously thank you for your information. The article has truly peaked
my interest. I am going to book mark your site and keep checking for new information about once
a week. I subscribed to your Feed too.
I enjoy looking through a post that can make men and women think.
Also, many thanks for allowing for me to comment!
I’m truly enjoying the design and layout of your website. It’s
a very easy on the eyes which makes it much more enjoyable for me to come here and visit
more often. Did you hire out a developer to create your theme?
Excellent work!
Hi there, I enjoy reading through your article.
I wanted to write a little comment to support you.
What’s up Dear, are you actually visiting this website regularly, if so after
that you will definitely get nice know-how.
Thank you for the auspicious writeup. It in fact was a amusement account it.
Look advanced to more added agreeable from you! However, how could
we communicate?
Its not my first time to pay a quick visit this
website, i am visiting this web page dailly and obtain fastidious facts from here every day.
After checking out a handful of the articles on your site,
I seriously appreciate your technique of blogging. I added it to my bookmark webpage list and will be checking back
in the near future. Please check out my web site as well and tell
me your opinion.
Every weekend i used to visit this web site, for the
reason that i want enjoyment, as this this web page conations actually fastidious funny information too.
Thank you for the auspicious writeup. It in fact was a amusement account it.
Look advanced to far added agreeable from you! However, how
could we communicate?
Great blog right here! Also your web site lots up fast!
What web host are you using? Can I get your associate hyperlink to your host?
I wish my website loaded up as quickly as yours lol
Great article.
Hi there to all, the contents present at this website are in fact awesome for people experience, well,
keep up the good work fellows.
I always spent my half an hour to read this weblog’s articles every day along with a mug of
coffee.
This article will assist the internet visitors for building up new website or even a weblog from start to end.
Great post. I was checking continuously this blog
and I am inspired! Extremely useful information specially
the closing part 🙂 I take care of such info much. I was seeking this particular information for
a long time. Thank you and best of luck.