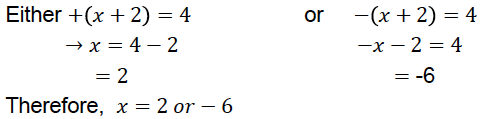NUMBERS II MATHEMATICS FORM 1
NUMBERS II MATHEMATICS FORM 1
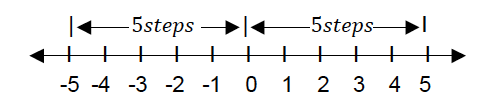
A Rational Number
Define a rational number
ARational Numberis a real number that can be written as a simple fraction (i.e. as aratio).
Most numbers we use in everyday life are Rational Numbers.
| Number | As a Fraction | Rational? |
|---|---|---|
| 5 | 5/1 | Yes |
| 1.75 | 7/4 | Yes |
| .001 | 1/1000 | Yes |
| -0.1 | -1/10 | Yes |
| 0.111… | 1/9 | Yes |
| √2(square root of 2) | ? | NO ! |
The square root of 2 cannot be written as a simple fraction! And there are many more such numbers, and because they arenot rationalthey are calledIrrational.
The Basic Operations on Rational Numbers
Perform the basic operations on rational numbers
Addition of Rational Numbers:
To add two or morerational numbers, the denominator of all the rational numbers should be the same.
If the denominators of all rational numbers
are same, then you can simply add all the numerators and the denominator value will the same.
are same, then you can simply add all the numerators and the denominator value will the same.
If all the denominator values are not the same,
then you have to make the denominator value as same, by multiplying the numerator and denominator value by a common factor.
then you have to make the denominator value as same, by multiplying the numerator and denominator value by a common factor.
Example 1
1⁄3+4⁄3=5⁄3
1⁄3 +1⁄5=5⁄15 +3⁄15 =8⁄15
Subtraction of Rational Numbers:
To subtract two or more rational numbers, the denominator of all the rational numbers should be the same.
If the denominators of all rational numbers are same, then you can simply subtract the numerators and the denominator value will the same.
If all the denominator values are not
the same, then you have to make the denominator value as same by multiplying the numerator and denominator value by a common factor.
the same, then you have to make the denominator value as same by multiplying the numerator and denominator value by a common factor.
Multiplication of Rational Numbers:
Multiplication of rational numbers is very easy.
You should simply multiply all the numerators and it will be the resulting numerator and multiply all the denominators and it will be the resulting denominator.
Example 3
4⁄3×2⁄3=8⁄9
Division of Rational Numbers:
Division of rational numbers requires multiplication of rational numbers.
If you are dividing two rational numbers, then take the reciprocal of the second rational number and multiply it with the first rational number.
Example 4
4⁄3÷2⁄5=4⁄3×5⁄2=20⁄6=10⁄3
Real Numbers
Define real numbers he type of number we normally use, such as 1, 15.82, −0.1, 3/4, etc.Positive or negative, large or small, whole numbers or decimal numbers are all Real Numbers.
They are called “Real Numbers” because they are not Imaginary Numbers.
Absolute Value of Real Numbers
Find absolute value of real numbers
The absolute value of a number is the magnitude of the number without regard to its sign. For example, the absolute value of 𝑥 𝑜𝑟 𝑥 written as 𝑥 .
The sign before 𝑥 is ignored. This is because the
distance represented is the same whether positive or negative.
distance represented is the same whether positive or negative.
NUMBERS II MATHEMATICS FORM 1
for example, a student walking 5 steps forward or 5 steps backwards will be considered to have moved the same distance from where she originally was, regardless of the direction.
The 5 steps forward (+5) and 5 steps backward (-5) have an absolute value of 5
Thus |𝑥| = 𝑥 when 𝑥 is positive (𝑥 ≥ 0), but |𝑥| = −𝑥 when 𝑥 is negative (𝑥 ≤ 0).
For example, |3| = 3 since 3 is positive (3 ≥ 0) And −3 = (−3) =3 since −3 is negative (3 ≤ 0)
Related Practical Problems
Solve related practical problems
NUMBERS II MATHEMATICS FORM 1
Example 5
Solve for 𝑥 𝑖𝑓 |𝑥| = 5
Solution
For any number 𝑥, |𝑥| = 5, there are two possible values. Either 𝑥,= +5 𝑜𝑟 𝑥 = 5
Example 6
Solve for 𝑥, given that |𝑥 + 2| =4
Solution
